The Ternary Logic Truth Tables
And here, we will turn our attention to the Ternary Logic Operators.
It is at this point that most definitions of tertiary logics begin their description, or at the very least, specify a representation of their values, such as -1, 0, 1 or 0, ½, 1.
Yet these symbolic aliases do not address any of the inherent ambiguities of the formal logic systems we have discussed so far, (the implied existence issue, or the ambiguity of assertion, for example).
Because they do not reconcile their tertiary forms with the bivalent principles of the fundamental Laws of Thought, their systematics are difficult to embrace, and their definitions have not garnered any significant acceptance.
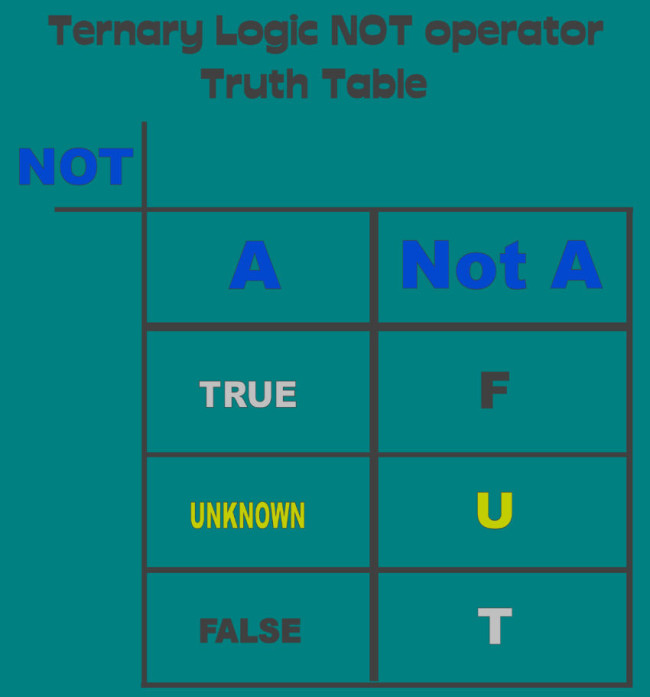
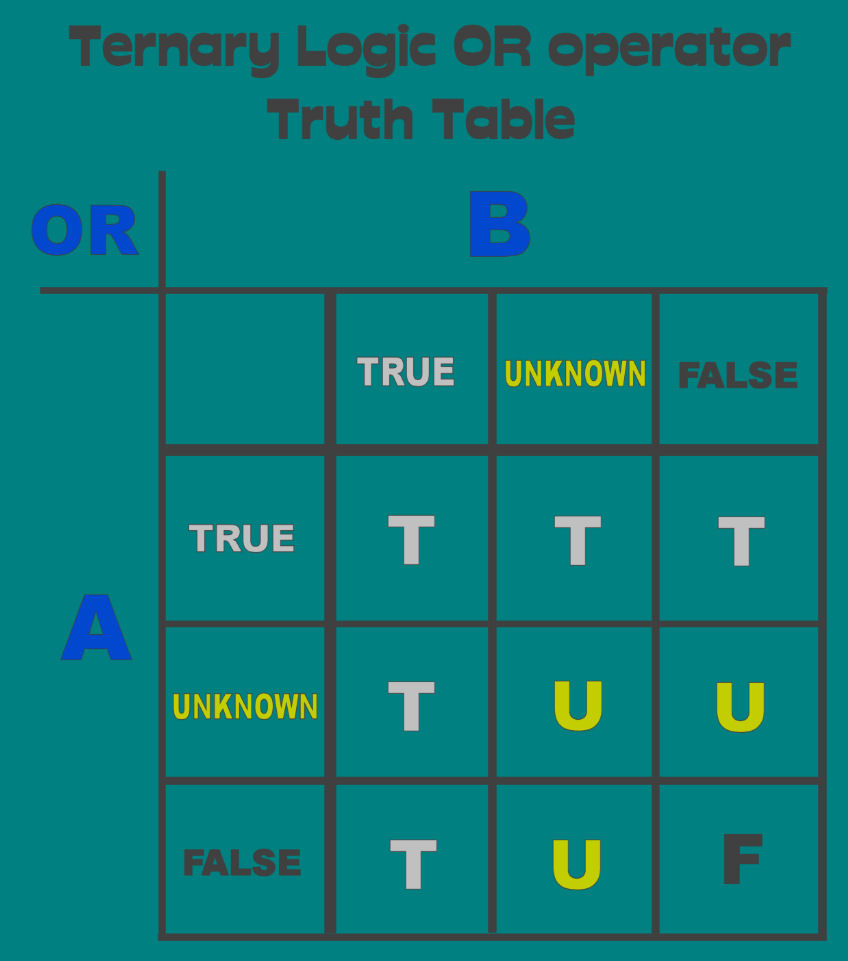
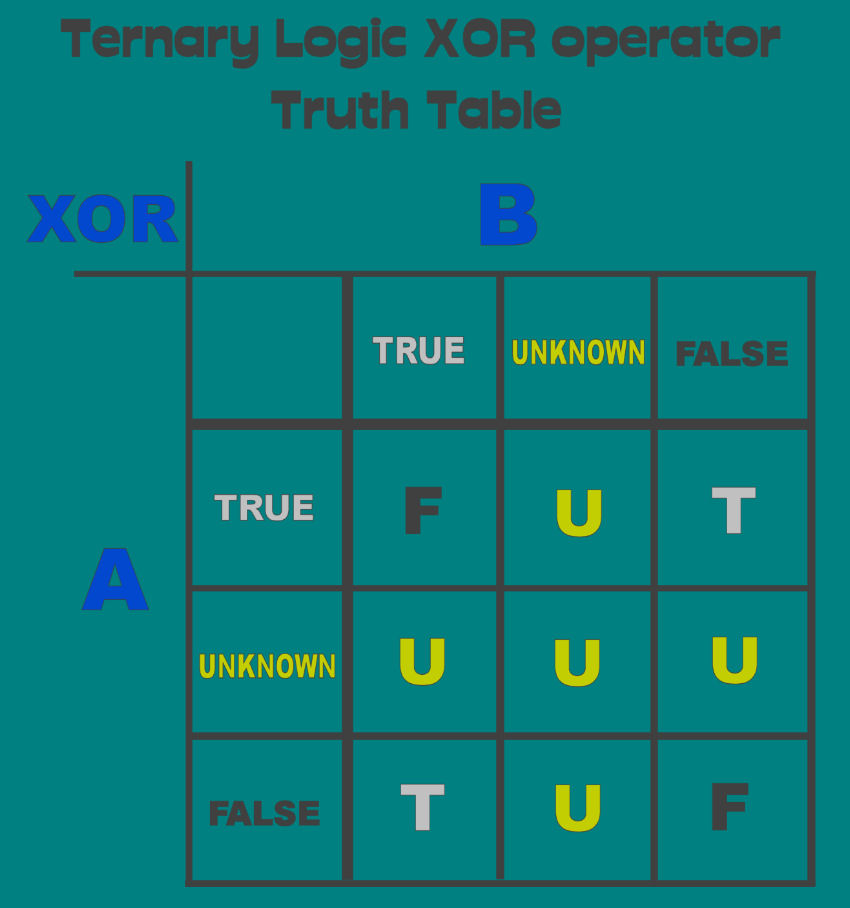
But they do possess some redeeming factors, and it is the truth tables of the strong Kleene logic that we adopt as our basis for the Ternary Logic Operators Not, AND, Inclusive OR, Exclusive OR.
Also, while here, in order to maintain some conformity with conventions, we will adapt the alias “False” for the logic state “Not True”, and will utilize that alias for the duration of the definition.
Definitions for the logical operators are best expressed in the form of truth tables, and so we present the Ternary Logic truth tables for the logical operators:
RETURN TO THE ORGANON SUTRA
RETURN TO THE LOGIC PRINCIPLES
GO TO TOP OF PAGE
Copyright © 2019 All rights reserved