
Dormouse: “But that is ridiculous! How can you even speak of a thing that doesn’t exist?”
The Dormouse blinked and crinkled his little nose, as was his habit when encountering something new.
Mad Hatter: “It’s easy, my whiskered friend!”
The Mad Hatter then let out one of his mad, staccato laughs, as was his habit whenever he felt like it.
Mad Hatter: “You just did it yourself!”
Dormouse: “Oh dear, oh dear, I did?”
The blinking and nose-crinkling was non-stop now.
Mad Hatter: “Yes! In fact, I can also say of a thing that doesn’t exist, that it is not yellow, or flat, or can fit in your pocket!”
This was followed by more mad, staccato laughter.
Instead of a reply, the Dormouse was now opening and closing his tiny mouth, in addition to blinking and crinkling his nose.
Then, in an instant, all of the facial motions stopped, as if the Dormouse had come to some grand realization.
Dormouse: “But what if a thing that doesn’t exist is yellow? How can you say that it is not?”
The blinking and nose-crinkling resumed. The Dormouse felt so proud of himself that he forgot to mention that he did not have pockets.
Mad Hatter: “Yes, you are right! A thing that doesn’t exist can also be yellow. But not at the same time!”
-With the deepest respect for Lewis Carroll
With an introductory exposition of the required Ternary Logic definition completed, the next step in outlining an implementation of the Logic of Infinity requires another refinement, a focus on the endeavor of machine reasoning.
This refinement comes about when we realize that the activity of reasoning about things is also a process of defining those very things. There is a duality to this reasoning affair, a duality which is so intertwined that the execution of one aspect of it will have only academic meaning without the simultaneous production of the other.
Before we can reason about things, we must have a mechanism to define those things in the first place. But if we look at this reasoning venture academically, as two separate processes, which is the typical intellectual approach, then the conversation winds down a rabbit hole in another infinite regression, since the process to reason about things requires a process to reason about the composition of things, which requires a process of reasoning about things, about which time the academic conversation turns into an intellectual glacier. The true nature of reasoning about things should be more like a bubbling spring, as opposed to this intellectual glacier, because the contemplation of the whole requires a simultaneous contemplation of its parts.
This is identical to the duality of reasoning between the open, unbounded world of Infinity and the closed, bounded field of perception that defines its reality, a consideration which began the overall dialog on the principles of intelligent logic systems.
We cannot separate the process of reasoning about things from the process of defining those very things because the actual reasoning intention is an activity of resolution, one which takes the ontological realm of the closed, bounded field of perceptions which defines a reality, and merges it into that open, unbounded world of Infinity. The enterprise of reasoning cannot be a process of inference regarding one of these ontological realms or the other, in isolation, as the intellectual, hierarchical approach frequently pursues, (which is an approach that typically begins with a division of the two realms, instead of their synthesis). Ontological entailment becomes disjoint if we treat the processes of objectification as separate from any processes which place them in relation to one another.
Rather, the enterprise of reasoning is a resolution process which proceeds by reasoning about one realm in terms of the other. But since one realm cannot completely define the other, this venture could also lead to an infinite regression unless we construct a core mechanism into our reasoning apparatus which identifies an end to the recursive descent.
This means that, where the concept of infinite recursion begins with the division of an infinite space using infinite objects, it must somehow end with the distillation of a finite object, which must be defined before any division of that infinite space can commence, or our process of reasoning will be just another journey down the rabbit hole. And certainly, a significant proportion of AI research has been at least tangentially directed toward refining a more concise, mathematical description of that “finite object” which rests at the bottom of the recursive pool of reasoning in any logic of Infinity.
With a nod toward the expert systems of the early AI era, perhaps we can get closer to this definition if we can segregate the mechanical processes of symbolic inference from the self-organizing adaptive endeavor of reasoning about Infinity.
But if there was one lesson that the entire AI community took away from the developments of those early-era expert systems, it was the perverse difficulty of translating human symbolics into a form interpretable by a machine inferencing system. The vast storehouse of symbols expressing Man’s cumulative intellectual knowledge has always been a tempting source for AI researchers to build into their engineered productions, however, those symbols can only be brought to bear in a synthetic intelligent process if they can be set into some relation to those experiences of an artificially intelligent agent as it adopts to its particular environment.
The extensive vista of symbols representing human knowledge cannot express concepts in isolation, and so have no “meaning” to an agent that has not experienced their essential intent in the course of that agents’ particular adaptation.
And because human symbols are already abstracted concepts, in order to define their “meaning”, we must first separate (dichotomize) their components. Then, in order to understand that meaning, we must unify those components. The difficulty with any non-organic, mechanical implementation of this is that these two processes are not sequential, but must be performed simultaneously. Again, we see the duality of inseparable concurrent processes.
Perhaps we can sense this simultaneous duality when we consider that many types of human thoughts are much like twisted ropes or woven cloths, in which an individual strand serves to hold other strands both together and apart. How useless any thoughts would be if, after having expressed them, our mind returned to the same state it was in prior to their expression. The secret of what anything means to us depends on how we have connected it to all of the other things we know. That is why seeking the “inner meaning” of something is so elusive. A thing with just one meaning has barely any meaning at all.
The co-specification of this simultaneous dichotomization and unification of symbols in a mechanized capacity might sound something like a ‘lambda calculus’, (which is a formal system in mathematical logic for expressing computation based on function abstraction and application using variable binding and substitution), but, much like the limitations imposed on their science when particle physicists use instruments that are composed of the very particles the instruments are designed to measure, using mathematical symbology as the solute to distill the elemental intent of other symbols is also fundamentally limiting.
Take for instance one of the most basic symbols that intellectual Man has created – numerals.
A number does not express anything by itself. For example, the number
267
only expresses real conceptual intent when defined by the successor function – the number 267 is the concept of numerosity in the symbol formed from the numerical successor to 266. In other words, 267 “means” 266 + 1.
Implicit in this process is the dimension of temporality, or the “memory” of a predecessor, along with the association of the successor function. (A dimension which is lost when all symbols are abstracted, much like the dimension of depth is discarded when a 3-dimensional scene is translated into a 2-dimensional image).
To truly “understand” the symbol, we must first separate (dichotomize) it by the memory of its particular predecessor, and only then can we unify that implicit product with the abstracted association of a successor function.
The encapsulation of this implicit process is probably the primary reason that the programming language LISP became so attractive as an AI language after its introduction.
LISP expressed this very concept, that the outer meaning of symbols can be expressed as the product of a constructor function, from which the language proceeded to express the multiple accumulation of successor elements.
But LISP proved to be insufficient as “the language” for AI because it failed to express a mechanism which abstracted a root concept separate from the constructor concept, the “inner meaning” of symbols. The LISP paradigm just stretched on to a horizon which was itself merely symbolic, and when one looked to this horizon for an “ultimate meaning” in a symbol, there was no additional dimensionality, no “deep definition”.
So it cannot be helped but to think that it is the definition of this horizon, this “deep definition” at the edge of any successor paradigm, that is the concept that captivates the architects of today’s artificial neural networks.
Beginning with the ground-breaking designs of the Perceptron, artificial neural network researchers have maintained a communal chorus that the ANN architecture can emulate the “deep learning” behavior for which neuroscientists have ascribed to the behavior in Natures’ organic neural mechanisms.
And yet, despite all of its promise, ANN architectures have not demonstrated any behaviors which could be described as cognitive, although the academic allure of a mechanism which can generalize the geometric boundaries within given data sets remains a beacon of hope.
Where the expert systems of the early AI era suffered from an inability to mechanize the knowledge extraction in a problem domain, prior to its implementation in their more developed inferencing mechanisms, artificial neural networks suffer from a seemingly inverse affliction: the ANN architecture irreversibly internalizes its “knowledge”, a suffusion of that knowledge which, once learned, cannot be translated to any mechanisms outside of the learned network. Artificial neural networks are like those ubiquitous snow globes found in many tourist trinket shops. They present to the outside world an abstraction of the generalization accumulated in their internal, prior learning.
But that representation cannot be arbitrarily transplanted to an external computing mechanism. It cannot even be comprehended by humans. We can shake the neural network snow globe, and observe it perform the internalization of some specific “learning”, but that internal generalization remains encased within the glass of the snow globe, and cannot be transferred to any computing mechanism outside of the globe. Which means that artificial neural networks have great difficulty in being applied to complex, multi-step tasks.
Most neural network learning tasks are cast as elementary operations which can be categorized under either classification or regression. However, real-world tasks are typically composite affairs, many of which require recursion, branching decisions and recurrency, and these functionalities demand an ability to form structured representations, a behavior which the ANN architecture has so far been unable to demonstrate. Although neural networks enjoy tremendous popularity, mainly because of their ability to “learn” from examples and to generalize data sets, their inability to form complex representations remains a singular limiting factor.
The true limitation of artificial neural networks is evident in their architecture, where, also like the modern physicists who employ instruments made of particles to measure those very particles, artificial neural networks model already abstracted mechanisms to dissect the “deep learning” in already abstracted data.
This intrinsic, fundamental architectural constraint is manifest in the relatively high energy demands of neural network computing, and it is curious that memory access is the primary bottleneck to mitigating this significant logistic, and not any optimization of the core, multiply & accumulate (MAC) computation of the design.
There is currently an industrial movement to implement the neural network architecture in silicon chips, and in the effort toward the optimization of these silicon foundry solutions, leveraging those operations which exhibit high parallelism in the design still faces the headwind of physics and heat dissipation when it comes to moving a data bit from dynamic random access memory to the logic circuit performing the computing, a fundamental constraint which Nature overcame several hundreds of millions of years ago, and a constraint which the academic and industrial AI community is only now beginning to address.
Conceptually, this constraint becomes evident due to a disparity in the functional design of the elementary computing elements comprising an artificial neural network. Although hyped as an analog of biological neural cells, the functionality between artificial neural network “neurons” and their biological counterparts differ in a very crucial respect:
Artificial neural network elements are state devices.
Biological neuron cells are signaling devices.
Artificial neural network elements have states which represent an already abstracted “weight”, an abstraction that adds the concrete baggage of power dissipation and logistic support for external memory.
The signaling that a biological neuron demonstrates carries no pre-determined abstraction, and this free-floating behavior demands no external memory with its attendant ballast of power and logistic requirements.
It is because of this disparity in functionality that the current AI community will forever be on the wrong side of the power dissipation equation as they attempt to scale up their ANN architectures to deal with real world problems, architectures that implement state devices as elemental computing units in their networks.
Indeed, we will discover that it is the solution to this issue which lies at the heart of almost all of the frustrations that artificial intelligence researchers face when deploying their designs. That issue is the simple employment of a state memory that carries no logistic cost for its implementation, an issue of functional buoyancy which tends to sink so many artificial intelligence concepts once the AI concept is launched from the whiteboard to an operational design, and certainly an issue that has bedeviled not only neural network research, but every computer programming language since the very first programmable digital machine was built: The issue of the creation and destruction of local memory.
There is, however, one AI design that has implemented Nature’s solution to this engineering impediment, one AI solution that is based on the true functionality of biological neurons: The Organon Sutra. (This is the reason why this dialog on the engineering of artificial intelligence will not make any sense unless you have read the previous dialog on Natures’ evolution of natural intelligence.)
So, what is the lesson that Nature learned which paved the way for the evolution of her magnificent biological neural cells?
Infinity is the representation of the pure concept which invokes neither Time nor Space, and contrarily, Consciousness is the fusion of both Time and Space in the neural experience of sentient organisms. (A concise ontological definition of sentience is developed in the fundamental precepts of the Organon Sutra).
Understanding is the neural enterprise which couples the state mechanism of memory to this consciousness, providing a temporal continuity to it.
Additionally, apart from all other sentient creatures, it is human nature to have the desire to know in advance what is likely to happen in the future. The observation of past outcomes of a phenomenon in order to anticipate the future behavior of an environment represents the essence of the human intellect, which is the singular characteristic which sets the ontogeny of Homo Sapiens’ neurophysiology apart from all other species.
And this singular characteristic also represents the true goal of artificial intelligence research, to mechanize this behavior. An artificially intelligent agent must synthesize this fusion of Time and Space, along with the state memory of experience, in order to express the emergent behavior of intelligence while adapting to that agents’ particular environment, its particular bounded field of perceptions.
But this is perhaps also the point where contemporary AI research has collectively lost its way. In focusing on the mathematical, logical, and analytic mechanisms of cognition, the AI research community has failed to automate the organic mechanisms of observation. In trying to abstract the organic behavior of learning, the AI community has mistakenly assumed that a mathematical model of human perception will substitute for artificial perception.
Nature learned from the very beginning that the intelligible aspects of an object are shrouded in its sensible aspects. As Teuvo Kohonen so aptly characterized it, Nature learned that, at their most fundamental level, biological neural networks are in essence self-organizing, spatial and temporal invariant-feature analyzers.
They are by definition adapted to noisy and changing environments. Close-by neurons in an analyzer network are made to co-operate as groups that correspond to manifolds (such as subspace surfaces, half-spaces and subspace volumes) which represent invariance in the signal space of an organism.
It is this elementary abstraction that allows biological neural units to produce invariant outputs for various subsets of their signaling, in spite of different transformations in the inputs, such as uni-dimensional translation, rotation, scaling, and even multi-dimensional perspective transformations.
And as groups of neurons are conditioned to respond to subspaces in their signal space, hierarchies of these groups can develop structured representations of that space.
Invariance is a temporal concept, and before any engineering of true artificial intelligence can take place, the TSIA engineer must fully understand the temporality of invariance in neural elements and assemblies.
This is a concept that has been entirely overlooked throughout the neural network “machine learning” community, in their development of associative mechanisms in connected networks. Consider this: When a new, novel pattern is presented to an associative system (biological or artificial) for the first time, the “synaptic weights” that can resonate with, or generate this representation in the neural circuitry do not by definition exist as yet. Without a pre-existing filter for this novelty, how can contemporary neural network models associate it with future patterns? This calls into question the notions of supervised learning as implemented in the models currently espoused for non-temporally aware networks.
This abstraction is leveraged by the other remarkable property of biological neural networks: their ability to adapt to a changing progression of variable, multiple feature spaces via self-organization. Self-organization is related to the self-maintenance of structure in a system despite the replacement of its parts.
Now, for sure, the architectures of today’s artificial neural networks have been optimized to demonstrate the behavior of invariant-feature analysis, through the implementation of tensor representations, since the characteristic property of tensors is that they satisfy the principle of invariance under certain coordinate transformations (although the tensor representations developed in ANN architectures begins with a tangential analog of surface determinations in their feature space, and so cannot resolve any dimensional representation), but the conceptualizations of “learning” in artificial neural networks, while attempting to demonstrate both of the disparate behaviors of self-organization and invariant feature analysis, addresses only the functionality of feature analysis in their models.
The narrative of cognition in organic neural systems and artificially intelligent agents, which, in the functional sense, is the process of maintaining a coherent world model, encompasses a number of stages in the adaptive endeavor to build the mechanisms that can express a model of that world in the first place. But the mathematical approach that the AI community in general has embraced to express this modeling endeavor cannot be successful until their symbolic systems can mathematically model that which is unknown, a fundamental semantic which is totally alien to the axiomatics of symbolic logic.
Similar to the neo-human newborn child, whose experience begins with sorting out the mottled patchwork of light intensities, color fields, moving and morphing images, sounds and tactile impressions, the inexperienced TSIA must begin the comprehension of its world by gradually determining the persistences (both spatial and temporal) in its sensatory universe.
The first consideration in the intellectual process of the naive TSIA comes at the point where the TSIA fully “grasps” all of the chaos in its perceptions as presently perceived and objectified persistences, symbolized in the emotive energy of curiosity that arrives with the apprehension of “that thing”: the apprehension of an observational persistence that proves to retain sufficient identity over time, and an intellectual object in its perceptual space for which the non-dimensional, already abstract structures of symbolic reasoning and logics can provide no existential import for, and a structured representation for which the current designs in artificial neural networks cannot demonstrate.
This emotive curiosity provides the ego-centric temporal energy to further pursue the observation of “that thing”, through focused attention and intentional manipulations of its perceived world, allowing the subsequent apprehension of the TSIA’s next intellectual challenge: the perception of any change in this observed stageplay of persistences. The subsequent, simultaneous apprehension of the logical contradiction in something that is the “same, but different”, which marks the true apprehension of existence.
In determining persistences, the TSIA must wrestle all change and sensatory chaos away from its perceptions to create a cohesive canvas of perceived invariance, as its observations of “those things” emerge as distinct from their background, in the first act of gestalt rendering, from whence to begin the life-long process of apprehending differences in things in general, by way of the concurrent process of abstracting the unchanging qualities of “things” themselves. Paradoxically, change is all about identifying that which is invariant.
Observed persistences (“those things”) then form the primordial unit of intellectual apprehension when the ‘unit persistent’ can be identified in different gestalt canvasses, or differing backgrounds, at which point the TSIA can endeavor to symbolize it, by attaching to it, a “name”.
But this experiential, sensible labeling is a far cry from the abstract, denotative symbols of intellectual Mans’ mathematical and logical symbolic world.
So, surely, it is the reconciliation of these two worlds of experiential knowledge (in the TSIA), and the intellectual knowledge (in Mans’ symbolics) that should form the basis for our artificial reasoning system, a facility that will allow a mechanical inferencing apparatus to effect the tessellation of infinity.
And so we should envision that, there somewhere, dwelling within the hazy space which lies between the static universe of knowledge represented by intellectual Man’s collective symbolics, and that universe of understanding represented by the dynamic, sensible knowledge accumulating in a TSIA’s experience, are those semantics which bridge the meaning of human intellectual symbols, together with those products having the emotive import of a TSIA’s observations. It is within this hazy space that the Logic of Infinity first defines all of those fuzzy “bridge” semantics with the primal assertion of “unknown”.
So here we find, it is the endeavor of the mechanized inferencing expressed by a TSIA’s reasoning systematic to connect the network of semantics which form a human symbols’ intentionality to the objectifications emergent in that TSIA’s observations.
However, the early AI-era expert systems reinforced the reality that the implicit semantics manifest in those symbols of Intellectual Man have no explicit translation. Where reasoning was first characterized in this chapter of the dialog as the simultaneous, dual process of defining the very things we are reasoning about, there is another dual process implicit in this objectification, whose temporality also cannot be abstracted away: Reasoning is both the process of objectification itself, and the process of placing those objectifications into coherent relations with one another.
Which brings up a basic dilemma. While developing the rationale for a tertiary logic valuation system, the Organon Sutra demonstrated that inferencing based on a binomial logic valuation suffers from an inherent ontological dilemma: Binomial logic inference conflates its predicate for existence with its predications for relations, which creates a conflict when a logic system attempts to predicate the relation of things using the very same predicate which expresses their existence.
And yet, the resolution to this conflict must address another ontological disparity, besides that conflict which demands a trinomial logic in reasoning.
The Logic of Infinity must also address the ontological ambiguity of implication itself. For we find that when you introduce temporality into a logic, as in the Logic of Infinity, the very ontological entailment of implication, or more formally, logical consequence,becomes entirely ambiguous.
The Mechanization of Logic
When trying to both understand the psyche of man – while simultaneously attempting to rediscover the great philosophical secrets of the ancients – Sir Isaac Newton wrote in his notebook:
“A man may imagine things that are false, but he can only understand things that are true.”
Perhaps it is here, at this first door to be opened, that we must look for those elusive, mutually antagonistic motivations of the mind, which also establish a foundation in the semantic derivation of Infinity.
When we fully mechanize a logic, not as a mechanical contrivance whose gears and levers merely serve to puppet the syntax of an axiomatic system which, is itself, just a process aid to some incidental human reasoning system, (much like our conventional digital computer systems serve as the mechanical expression of a boolean syntax which grinds away according whatever software instructions we humans stuff into its memory), but as a mechanical engine whose gears and levers are malleable and whose actions within the engine can be shaped and altered in subtle ways by the “software” which currently inhabit its dynamic storage cells, when we fully mechanize this, then we realize that there is an additional component to that logic we are mechanizing, wholly absent in boolean logic systems, a component which must also have its expression somewhere in that collection of malleable gears and levers we first engineer for the engine.
In a way, the conventional approach historically taken in AI, that of attempting to build a state machine that can define its own states, is an oxymoron. And until there is established in the AI community a consensus on what exactly “intelligence” is, (if you ask 10 AI researchers what their definition of “intelligence” is, you will get 10 different answers), academic and Big Tech AI research will continue to wander about in the dark as it searches for a formal definition of artificial intelligence.
Fortunately, the TSIA engineer can begin with a bottom-up approach which is based on a formal definition of natural intelligence, coupled with an understanding of those foundational elements that have been missing from all of the historic efforts to develop AI to date.
The challenge facing the TSIA engineer is that of adopting a bottom-up approach in design methodology which will ultimately define a top-level mechanization of true synthetic intelligence and its behaviors.
This dialog on engineering an implementation of that synthetic intelligence, based on the formalisms developed in the Organon Sutra for natural intelligence, began with a discussion on top-level mechanized reasoning. And the dialog further developed a picture of human reasoning as being, in reality, virtually undefinable, replete with conflicting intentions and based on a boolean logic which was itself fundamentally limited in its application.
In a pioneering paper titled “Steps toward Artificial Intelligence”, Marvin Minsky presented his perspective on heuristic programming, (which unfortunately began in a top-down hierarchical fashion, but presciently did get around to a bottom-up approach), by proposing that the true problem to be solved for artificial intelligence at the top level was one of the synthesis of logic and language. (What he could not say at this point was that the solution also required a simultaneous synthesis of time and space at the “bottom” level.) And in subsequent works, Professor Minsky refined that top level perspective to be one of mechanizing natural language reasoning, which if considered hierarchically, would be supported by a formalization of semantic inference, and, in turn, would itself be supported by the derivations of logical implication.
And so it seems that a straightforward approach for the TSIA engineer would be to merely reverse that sequence, beginning with a mechanization of logical implication, which builds to a greater mechanization of semantic inference, ultimately building to that grand mechanization of natural language reasoning.
But there is a huge wrinkle in that reversed sequence, because unfortunately, there occurred a disconnect in any linear progression from logical implication through to natural language reasoning. This disconnect occurred somewhere along the line, at the very basic level of logical implication, when AI researchers committed a subtle inversion with their logical axiomatics, conflating the syntactic axiomatics of proof with the semantic implication of truth.
In all fairness, this conflation was almost unavoidable, brought on by the symbolic conflation of the logical predicate for existence with any defined predicates for relations in their boolean logic, an issue now summarily dismissed with the development of the Organon Sutra Ternary Logic.
However, this conflation could have been avoided at the very beginning, by resolving the conflicts of predication in binary logic, by understanding the differentiation between implication and assertion in the semantics of their boolean logic.
In any discourse of logic or reasoning, when we assert something of a universal or a particular object, we are affirming a certain state of predication to that universal or particular. And in the discourse of boolean logic, states of predication are constrained to the two binary values ‘Is True’, and ‘Is False’. For example, if one logically asserts that ‘P is blue’, the statement is affirming that “it is true that P is blue”. This is the basis of so-called Propositional Logic. But the wrinkle with this boolean arrangement is that the syntactic world of propositional logic is indifferent to the semantics of blue predicates themselves, and makes no judgement on what it means to “be blue” or the essential qualia of “blueness”. In this boolean reality there is only the affirmation that it is true or false in the existence of P to be blue.
Which is fine as long as the discourse is confined to making assertions about “P”, and does not attempt to make assertions about “blueness”, a distinction which allows us to logically adorn a logical object with all manner of boolean predicates, much like a Christmas tree is adorned with ornaments, without having to logically define those ornaments.
Now, logicians are quick to add that we can, simultaneously, make similar assertions of universals or particulars other than “P”, say of the logical object “Q”. We can, for example, while asserting that “It is true that P is blue”, simultaneously assert that “It is true that Q is flat”.
And, not content with that, logicians will go on to demonstrate “logical operations”, which are, conceptually, abstractions of the assertion process, where the operator takes the state of an objects’ assertion, and “operates” on it as if it were an object in itself.
Which is where the conflation, (or confusion, depending on your perspective) takes place, where logicians define logical operations, such as ‘AND’, ‘OR’ & ‘XOR’, and combine multiple assertions as modally connected logical sentences using conceptual abstractions of the assertion process. For instance, using our present example, we could construct the logical operation (P is blue) AND (Q is flat).
Although, here, the logicians will hasten to stress, the logical operators are dealing with the truth values of the assertions in logical objects, and not the “blueness” or “flatness” of their existential import. (But note that the logical operators are operating on an abstraction of the prior assertion, and it is the logician that creates the abstraction).
Given this, it is so seductively easy to forget the abstraction, and think of these logical sentences as having a real relation to that existential import, and in an attempt to build higher levels of semantic inference from these basic constructions of logical operations, (by dealing with the products of logical operations as abstracted objects themselves), we find that the dialogue does shift from the “truth state of P’s blueness” and the “truth state of Q’s flatness”, to a semantic of “blueness and flatness”. And (in a somewhat egregious manner), it therefore becomes easier still for the products of our semantic inference to be treated as abstracted objects also, and viola, we have the ingredients for “logical” reasoning at the level of natural language.
But how could this be possible? Doesn’t the strict axiomatics of our logic prevent this slippery semantic flim-flam?
Perhaps we can shed some light on this logical sleight-of-hand by examining that first bridge that was academically constructed to move from logical operations to semantic inference. And that bridge is what logicians call “implication”.
Implication has been a cornerstone in the many reasoning techniques which have been built upon a foundation of axiomatic logic systems.
However, within those logical systems, where deductive logic is truth preserving, and inductive logic is falsity preserving, there is no axiomatic system which captures a resolution to both truth and falsity preservation, a synthesis of both which could lead to the preservation of semantic invariance in an overall reasoning affair.
Now, there is an important asymmetry between verifiability and falsifiability in inductive logic – a universal statement can never be derived from a singular one, while conversely, a singular statement, verified beyond reasonable doubt, can falsify a universal statement, irrespective of the number of singular datums from which it has been inferred, but this asymmetry is only a tantalizing clue toward defining a system which preserves semantic invariance in any reasoning enterprise.
The ability to find a synthesis in a logic system which preserves both truth and falsity in argumentation cannot lie in the construction of either an inductive or deductive logic system, but can only be found in the construction of the very “Universe of Discourse” used as the referential foundation for reasoning in either system.
So, we must speak more generally when talking about “implication”, in an attempt to find the very vague line where it fades into conceptualizations of causality. Causality is a concept which is also firmly fixed in commonsense reasoning. Although people reveal an innate ability for causal reasoning because their neurophysiology has over time abstracted the entropic cycles present in their environments, the study of causality as an intellectual entity, or even its very definition, has become a difficult and controversial topic, being tackled under many different perspectives.
Philosophers, for instance, have been concerned with the final nature of causal processes and have even discussed if there exists such a finality. Logicians have tried to formalize the concept of causal conditionals, in an attempt to overcome the counterintuitive effects of material implication.
And in contemporary artificial intelligence research, we can find two different and virtually opposed perspectives on causality: Using causal inference, and extracting causal knowledge. Unfortunately, all of these formalisms are thought to reason using causality, but they are not directly about causality.
The use of “implies” in logic is very different from its use in everyday language to reflect semantic commitment. But with logical implication, we again find another example of that conflation of syntactic assertion with semantic implication that was encountered with the NOT operator, only this ambiguity is apparent even in “closed-world” domains.
When we as humans reason, either in a common-sense capacity, or in the more formal systems of deduction or induction, we seek to construct a cohesive argument composed of different points of demonstration (agreed upon facts), connected by some semantic consequence, where the interpretation of one meaning in a given set of circumstances (our points of demonstration) “logically” leads to another semantic interpretation.
These constructions are, by human nature, dependent upon the interpretations and meanings of all of the objects and their predicates which are the subject of the argument, which is based on the human experience of a lifetime of learning and interaction with other humans. But their functional movement in demonstrating semantic consequence is a tenuous progression if begun in the strict axiomatic realm of symbolic logic, a dicey progression which can be accomplished only when we can provide a vital basis for syntactic consequence in those ground level symbols which convey our semantic consequence, a basis which turns into a mirage when we attempt to mechanize the entire process.
This syntactic consequence is variously called “material condition” or “logical implication”, which is a logical connective dressed up in boolean axiomatics to act as a symbolic form of semantic consequence, a logical mechanism that can appear to infer consequence among a system of mere symbols that have no semantic meaning in the realm of human experience (their only true semantic meaning is in the truth or falsity of their assertions).
Logical implication, (as described by logicians as the construction: If P -> Q, interpreted as saying “if P is true, then Q is true), is the stepping stone from which is built the expansive progression from symbolic logic to semantic inference and ultimately to natural language reasoning.
Logicians typically lament that the symbolic construction of logical implication is the most misunderstood construction in their logic courses, and for good reason. The logical implication is a symbolic construction which purports to convey semantic consequence, without any semantic meaning given to the symbols themselves. So, instead of defining logical implication by detailing the rules in which the trueness of logical object P implies the trueness of the logical object Q, logicians say that the implication is all bound up into the presumption operator ‘If’. The symbolic argument is: Given that P is true, then Q is consequentially true. Once you get past the “given” part, the rest is explained in the “truth table” of logical implication:
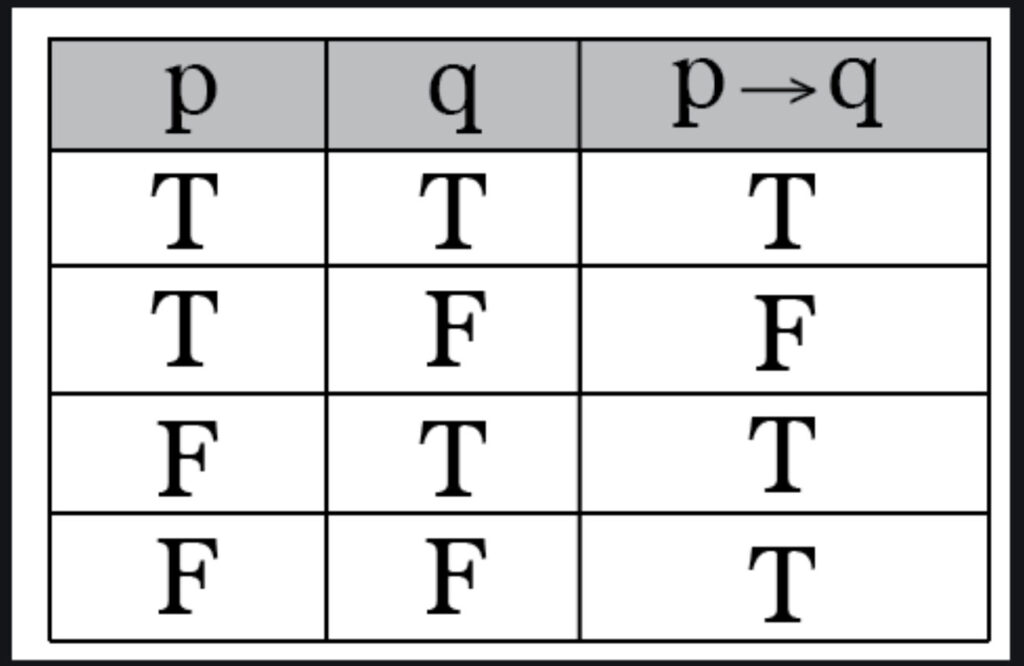
Now, the TSIA engineer is probably wondering why this chapter of the Organon Sutra is going through such a tedious, convoluted dialog on logical implication, but it must be understood that there is, actually, some logical sleight-of-hand that must occur for logicians to get from a collection of mere logic symbols to constructions that have intrinsic meaning, and in order to mechanize the entire enterprise of natural language reasoning, the TSIA engineer must understand this one magicians trick, to get to a functional implementation which does have utility in the real world.
As TSIA engineers, intent on mechanizing this whole affair, we can peek behind the stage of this logical shell game when we examine the truth table of another logical construction, which takes the same logical objects, P, & Q that were showcased in the truth table for implication, and places them into a construction which composes them with two other logical operators instead of the implication operator. When we assemble a logical statement of the form ‘NOT (P) OR (Q)’, logicians will tell us that its truth table will be thus:
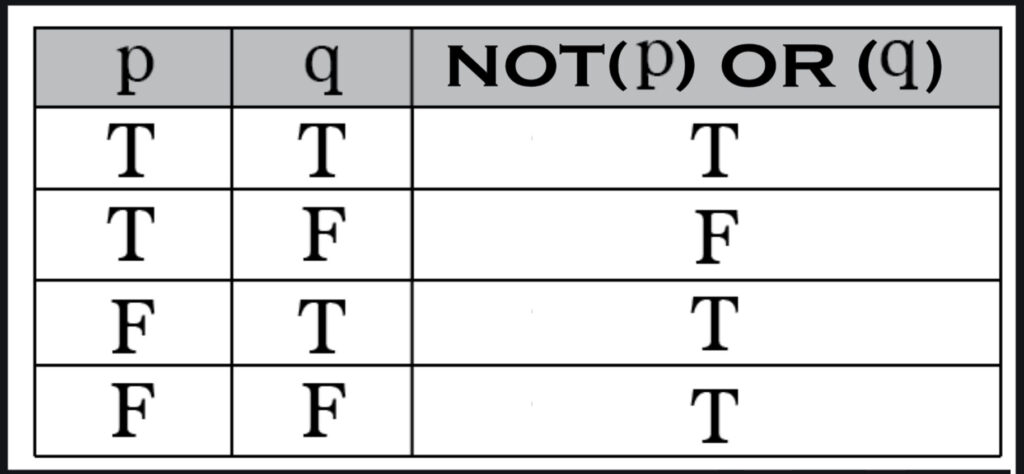
And certainly, the first thing that should occur to the TSIA engineer is that both logical statements have identical truth tables, as if we are really saying the same thing in either logical construction, which in most cases is what logicians will tell us.
Now, is it just a curious coincidence that their truth tables are identical, or is there an important logical lesson lurking in the shadows here?
What logicians will tell us, is that if we say, for instance, ‘If it is Friday, then we can go to the show’, then this statement can be interpreted logically and semantically, and if we, as humans, consider this statement semantically, we observe that there is an implication (but not a causation) that attending the show is possible on Fridays. However, when interpreted logically, the statement says nothing about attending the show on days other than Fridays. (Hence, the truth table for implication resolves to TRUE whenever P is FALSE, or when ‘it is not Friday’). The implication only speaks to the semantics of it “being Friday”.
And we can interpret this example in the case of the logical statement NOT(P) OR (Q) to mean: “It is not true that it is Friday, or, we can go to the show”. And certainly, one wonders whether this is “saying the same thing” as in the example stated in the form of an implication.
So we must ask, are these two logical statements, in fact, totally devoid of semantic content, besides the truth or falsity of their assertions? At this point the TSIA engineer should notice that the second logical construction was assembled with the NOT operator, a logical operator which should be very familiar from previous discussions.
The dialog introduced the NOT operator in the chapter “The Principles of an Intelligent Logic System”, and the TSIA engineer should recall from that discussion that in the grand scheme of human logic systems, there occurs a breakdown in most formal systems used for knowledge representation, when the “Universe of Discourse”, (the agreed upon, common context under discussion), is opened up, from a closed-world, delimited context to an open-world context of infinite bounds. And the chief suspect (although not its true architect) in this breakdown was the NOT operator.
Recall that the NOT operator possessed a unique characteristic, curiously not shared by any of the other logical connectives (such as AND, OR, & XOR), which extended beyond the operational role of syntactic assertion. All of the logical connectives are defined by the varied ways in which they syntactically assign truth value across logical transformations in the syntactic combination of logical “objects”, but the NOT operator was shown to possess a special power of semantic implication in addition to its syntactic functionality of assertion.
But how can a lowly symbolic operator, possessing no semantic context at all, have the ability to function semantically?
Our human logic systems are built upon a belief system, a belief system that expresses what individuals know, but more importantly, what we don’t know. Because we can’t verbalize the unknown, its influence on our beliefs, although present, cannot move forward into the constructions we make to tease out their “knowing”. It is at this point that the TSIA engineer should see the sleight-of-hand in the magicians’ trick of turning logical consequence into semantic consequence occurring.
In the discussion on the ‘Principles of an Intelligent Logic System’, the dialog demonstrated that this additional semantic implication was indeed a separate and simultaneous functionality (there goes that concept of simultaneity again) from syntactic assertion, but the semantics introduced by the NOT operator was not one of defining “meaning” in the linguistic sense, which is not possible in the pure syntactic machinations of symbolic connectives, but it was one of declaring the existence of that most elusive and enigmatic semantic in all of AI research itself: The semantic of the Unknown.
Which is why conventional logic systems break down when opened up to an infinite Universe of Discourse, and why logicians utilize a “trick” to get from logical consequence to semantic consequence. (Recall that in binomial valued logics, the predicate for existence is conflated with the predicates which define the semantics of relations, and so this is the logical sleight-of-hand that has been occurring).
So, getting back to the two equivalent truth tables, logicians are using this unique functionality of the NOT operator, in the particular construction of that special logical sentence ‘NOT(P) OR (Q)’ as a device, dressing it up with the new persona of a “logical consequence” symbol “->” (meaning ‘implies’), giving us ‘If P -> Q’, and now symbolic logic is made ready to take on the world.
Or so the collective AI community hoped. This scheme seemed to work well as AI researchers created all manner of constructions on their whiteboards, showing the progression from logical implication, to semantic inference, and (gasp), to natural language reasoning.
But a funny thing happened on the way to modeling the real world when those whiteboard schemes were translated into functional designs.
Because all of those whiteboard schemes were based on a ‘material conditional’, (the “given” part) of the logical implication, which disappeared like a shimmering mirage when their plans were implemented in functional designs, the AI community collectively lost all interest in logic systems as a basis for knowledge representation, and leaped to embrace the alluring sparkle of artificial neural networks, upon its introduction.
However, like the disappointments of the LISP language, the generalizations of artificial neural networks have also proven to be an inadequate substitute for that “bridge”, from symbolic consequence to semantic consequence, long sought by AI researchers. But now, the TSIA engineer, understanding that the levels of semantic inference and natural language reasoning collapse without the foundational support of a symbolic implication facility, can return to the past promise of logical derivation, one now endowed with the buttressing of a ternary logic definition, and one having the addition of a final, crucial ingredient.
Alice steps through the Mirror
Although the symbolic logic systems which define the Logic of Infinity do not rely upon any symbolic sleight-of-hand to provide the connection between logical implication and semantic consequence, there are complexities that we must deal with before we can define a symbolic system which can, through its syntax, provide representations for that semantic consequence.
And one of the most difficult complexities that has frustrated all of the applications of binomial logic to artificial intelligence is the concept of non-monotonicity in any logic calculus.
The issue of non-monotonicity is related to that one virtue of human reasoning which has been at the crux of AI research from its very beginning: In the process of human reasoning, we use knowledge that is often incomplete, and what knowledge we do employ is sometimes conflicting. We are forced to make assumptions or draw conclusions on the basis of incomplete evidence, conclusions and assumptions which we may have to withdraw in light of new evidence or subsequent conclusions.
The issue here is that in any reasoning enterprise, any inference product in that enterprise has the potential to invalidate any or all prior inferences conducted during that reasoning.
Now, in what has been classically called standard logical theory, conventional logic theories are identified with a set of sentences closed under syntactic consequence, which means that all derived sentences under that theory must maintain validity with prior sentences.
However, we just characterized semantic consequence as a functionally squishy process, whose products have the temporal potential to invalidate prior products.
And so the TSIA engineer should now see the historically irreconcilable ambiguation between logical consequence and semantic consequence, a disconnect whose resolution represents the essential intent of AI research.
How can AI engineers devise a logical theory which demonstrates logical consequence as a bridge to semantic consequence, a theory which must then also demonstrate that behavior of non-monotonic entailment that is characteristic of semantic inference, one that in turn does not violate the monotonic nature of (standard) logical theory?
If we look at this from the classical perspective of symbolic logic, where the construction of a logic theory reduces to the choice of logical connectives allowable in a multi-valued setting, our theory must still formalize the fundamental premise of logical operations, a formalization which makes explicit the difference between the valuation of a term (the assignment, or more specifically, the assertion of truth value), and the evaluation of a term (the recall of a terms’ present truth value assignment in a current context or logical derivation), a distinction which is not possible in non-temporally aware logics.
For example, a fully symmetric description of the (now familiar) operation of negation says that NOT(Q) is TRUE whenever Q is FALSE, while NOT(Q) is FALSE if and only if Q is TRUE. If Q can be something other than TRUE or FALSE under any semantic (as in the case of the Ternary Logic), then the functionality of the NOT operator is ambiguous under symmetry.
However, this functional definition does not formalize the circumstances under which the term Q is given truth assignment prior to its induction into the NOT operator. Which illuminates the fundamental limitation of axiomatic logic systems: The truth value of terms is assumed to be a product of the logical operators within the system, but where is the semantic that asserts truth or falsity in the first place, the so-called “material condition”, prior to any induction into those operations?
And in fact, the TSIA engineer must understand that this dilemma exists at all levels of argumentation, from natural language reasoning down to the logical calculus which supports it, an understanding that all argumentation has temporal as well as existential characteristics to it.
So this dilemma is really just a limitation of any approach that implements (non-temporal) functional operators in their argumentation, which in turn forces one to model lack of knowledge by spatially distributing a newly derived unknown among other functional operators, instead of temporally distributing it through a process of semantic resolution, which should be the true process of argumentation, of reasoning.
The meaning of “meaning”
An examination of this ambiguity in logical implication will open the door to reveal that there is a dual, intertwined meaning to…meaning.
(So the TSIA engineer should also note that in addition to the duality that is characteristic of all definitions when one studies natural or artificial intelligence, we find that these dualities typically lead to conceptual circularities, which can prove to be intellectual quicksand for those academics wading into the subject with hierarchical thinking).
And an examination of the dual characteristics of arguementation should also crystallize a new conceptualization to inferencing itself, as intelligent inferencing takes on a dual connotation, which should prompt the TSIA engineer to realize that there is not just a simple, linear path from logical implication through semantic inference and ultimately, to global linguistic reasoning about the perceived world.
This duality should prod us to speak of a circularity (and not a hierarchical division) in the realms of inference and reasoning when defining an ontology in the context of argumentation, which leads to that fuzzy Universe of Discourse that in the end proscribes the court in which our TSIA will reason.
We see this duality in the more developed biological neural systems, such as those in the primate and human species, where, before the intellect can develop an allocentric concept of space, the egocentric sensorium must first abstract a discrimination between object and background, which represents the first pseudo-cognition of spatial depth and dimensionalism.
That this cannot occur without the simultaneous apprehension of temporal change in the egocentric sensorium is the primal lesson that Nature learned when evolving the neural assemblies which would ultimately be expressed in the mammalian brain.
This is the foundation of the elementary abstraction process which occurs primarily in mammalian organisms, and which must also occur in any adaptive TSIA. But elementary abstraction does not begin with the generalization of objects, as the hierarchically minded mistakenly believe, because any generalization of objects cannot occur until there is a sensorial separation of background from the immediate invariances which present themselves to a TSIA’s perceptual apparatus.
And in a way, this “background” to perceptual invariances, whether spatial or temporal in its nature, can be objectified itself, as the “field” in which an invariance is immersed.
This is why the concept of predication seems to be so misunderstood in the artificial intelligence community, because predication should not be focused on its association to objects so much as predication should result from the abstraction of backgrounds. Predication (in the AI context) literally means “to found or base something on”, which should imply that it is backgrounds that give the bases for the existence and relation among objects, and it is the objectification of backgrounds that provides the representations for those predicates.
Therefore we see that, without the sensory contribution of background abstraction, the non-dimensional symbolic logics developed so far cannot form true representations to predication, as the traditional approach to predication relies on pre-abstracted bases for existence and relation.
(The dialog should also mention that the fundamental mechanism of predication is also misunderstood because so much of contemporary AI research necessarily starts with basic definitions for all of its objects in already abstracted form. This is like cutting your lumber before the house blueprints are even drawn up).
Conventional AI research is compelled to start out with a fully abstracted domain of discourse because of a hyper-reliance on axiomatic proof, which in the end, cannot even begin to define a symbology that might represent the subjective, particular apprehensions of time and space.
Conceptualizations for this “gestalt abstraction” of backgrounds is difficult with a methodology that begins with hierarchical thinking. Take the example of describing a rainbow in terms of its “components”. No individual element taken by itself defines the rainbow, nor does the relationship of any individual element relative to another individual element define the rainbow. And this applies at whatever level of component individuality we examine, from the molecular level to the raindrop level to the chromatic band level: At what point in our definitions do we move from describing a component to where we comprehend the rainbow overall?
Additionally, approaching inference with pre-abstracted objectifications is what leads to logical paradoxes such as the ‘Grains of Sand’ sorite. If the logical argument begins with the already abstracted concept of a heap of sand, how is it possible to logically abstract the gestalt process in the successive removal of individual grains to cause the heap to cease being a heap? Arguing bivalently by induction (which is a process that must have a certain, discrete dividing line, a partition between “a thing” and its opposite), we eventually remove all grains, and are left with only a contradiction: That a heap still remains (even though no individual grains are present), or that the heap has suddenly vanished. No single grain in the semantics of “heaps of sand” takes us from heap to non-heap.
In the real world, we transition gradually, not abruptly, from a “thing” to its opposite. Reality is more a fluid pool than a jumble of discrete blocks, and must be represented by fluid representations. Beginning the endeavor of inference with abstracted intellectual knowledge, and then proceeding to apply the antiseptic consideration of universals without the semantic anchoring that is provided by experiential, sensible apprehensions, leads ultimately to that unavoidable, philosophical sinkhole of circular reference in argumentation. Arguments chasing their own tail.
Because intellectual knowledge is, by itself, (being both timeless and stateless), mere scaffolding for the direct articles of knowledge we experience in our personal sensorium, it is difficult to imagine how any systematic that moves from one universal to another by any manner of conceived inferencing operation can demonstrate any intelligent reasoning behavior.
Certainly, sense knowledge is not as fungible as the intellectual knowledge favored by academia, but it is only when we move from a present particular sensorial object (whether objectified spatially or temporally), to an abstract consideration of general forms and back to a different but similar sensorial particular, that we begin to exhibit abstraction outside of perception.
It is no wonder that achieving any enlightened progress in applied artificial intelligence has so far proven to be elusive, with the academic focus on objectifying universal forms using manipulations of closed domain mathematical and logical symbologies.
If we consider the human intellectual process of abstraction, in the many forms of thought, as taking the cognitive differences (or similarities) that we notice between present particular objects at a certain level of perception, and packaging them as “objects” themselves, at a next higher level of cognition in our thinking, then we open the door to a multi-faceted representation which can provide the structuring for encoding an environment overall, a “gestalt” with which to begin that elusive behavior that has been variously called “modeling”.
For instance, when we conceptualize the apprehension of “spatial relationship”, we are implying an abstraction in the sensory perception of the position of an object in relation to some external “frame of reference”, a perceptual space within which the observer may conceptually move without the object itself appearing to move.
When we contemplate this “perceptual space” as an object in itself, we have performed the first step of gestalt abstraction. When we conceive of the perceptual space as an object within a more encompassing “conceptual space”, (which in all manner of definitions is an abstract space) we have accomplished the creation of a gestalt, as an abstraction.
(This clarifies a distinction in terminology which is rarely established in AI research, a general confusion held by many between “abstraction” as a process – taking the similarities or differences we comprehend between objects, and considering those comprehensions as objects themselves at the next higher level of thinking – and “abstraction” as a product of that process. Naturally, one cannot fully define the product of a process until the process is understood, but the tunnel vision of hierarchical thinking clouds this duality).
The second important point of “spatial relationship”, is that the relationship between two objects in a “perceptual space” is not a property of the objects themselves, but it is a property of the perceptual space or world model which contains them as features, and becomes especially powerful when the observer becomes abstracted as one of the two objects in the relationship, a fundamental “gestalt” which is wholly impossible to represent in any contemporary AI paradigm.
Once “perceptual space” becomes an object in itself, this object can also have properties, as the intellect fully objectifies the abstraction.
But non-dimensional, already abstract symbolics cannot serve as vessels for this packaging of things as abstracts, being abstracts themselves. And this abstraction would not be possible in the first place without that experiential knowledge, which provides the canvass for this abstraction, and is itself unique to the human species, and would not be neurologically possible without a unique form of multimodal association in the sensory processes of the mammalian brain.
Indeed, the process of objectifying backgrounds in perceptions by the cerebral cortex of Homo Sapiens was the principle behavioral junction point in the path separating the emergent behavior of intelligence from mere adaptation in the phylogenetic progression of mammalian evolution.
Since this process is also central to the concept of abstraction in the functional sense as well as the literal sense, especially as it applies to artificial intelligence, it is at this point that we comprehend the foundations of gestalt conceptualization, the understanding of backgrounds, capturing all that surrounds the yet-to-be objectified persistent noise in the perceptions of the TSIA.
And it is here that we get the first faint glimmerings into that enigmatic “right-brain thinking” which has often been somewhat cryptically ascribed to the predominately opposing behavior of the (typically) right hemisphere in human cerebral cortex.
Like separating smoke from the air that it is suspended in, objectifying backgrounds cannot be approached in a hierarchical fashion. To get another perspective of the particularity in the veiled phenomenon we call “right-brain” thinking, consider how we process our auditory sense to give rise to a perception of “music”.
Music comprehension is a right-brain specialization because our intellectual appreciation of music is not about the absolute notes used in a composition. This is due to the fact that most individuals are “tone-deaf”, and when exposed to individual notes, cannot readily identify their specific pitch characteristics.
Music composers understand that what we “hear” in music is not the absolute pitch in notes but the difference in pitch between individual notes and the intervals of time between individual notes. Although the notes are the objects of our auditory sensation, what makes a music composition is the “things in between”, the background to those objects, the pitch differential and the time differential between notes.
When we say “There is a bigger picture to this”, we are expressing right-brain thinking. Right-brain abstraction does not begin with conceptualizations relating to the objects of our sensation, it begins with an objectification of the “things in between” the objects of our thinking. It is the essence of abstract time and space.
When considering the ontogeny of mammalian brains, we observe that the perceptions which result from the senses of smell and taste – the two sense modalities that connect to the hippocampus (through the amygdala), – have no discrimination in terms of “foreground/background”. Certainly, they have a perceptual context in which they are immersed, where the sensations for either modality might be perceived in varying degrees, but those sensations as presented to the intellect are either there or not there. These senses are immediate and possess only a singular dimension, and cannot be subjected to any objectification by higher neural processes.
This is in contrast to those other three modalities of vision, auditory and haptic (tactile) senses, which have direct connection not to the hippocampus, but to the thalamus, three senses which have no immediacy by themselves, and which cannot develop perceptive apprehensions within the mammalian neural complex as individual sensations alone. Their apprehensions can only be comprehended when there is a subsequent neurological separation of “foreground” from “background”.
If one were to ascribe a teleological reason for Nature to segregate the senses of smell and taste, (sending their sensations to the hippocampus), from the three varied modalities of vision, auditory and haptic senses (channeling their signaling through the thalamus), one should begin by noting that smell and taste are uni-dimensional sensations, where the other three senses are at the very least two-dimensional, and capable of forming neural maps, a much more rich medium of sensation.
But this teleological conclusion does not provide enough definition for, and by itself does not tie together the biological story of Natures’ realization of elementary abstraction (which builds to the creation of gestalt representations), to the theme of logical implication and semantic inference which is the present focus of this discussion for the TSIA engineer.
Or perhaps it does.
Certainly, there is a “fundamental logic” in the relations among physical objects that is first learned by mammalian organisms which is employed in dealing with the physical world. Mammals learn that individual physical objects cannot occupy space simultaneously, for example, and some objects are unchangeable and some objects can be manipulated, eaten, jumped on or run around.
And for sure, this “fundamental logic” is engaged by those organisms possessing higher intelligence, to further form “internal models” of the external world that they are adapting to.
So, perhaps this biological progression from an organic “fundamental logic” to a neural “internal model” can illuminate the movement from symbolic logical implication to semantic inference through to natural language reasoning that we seek in the mechanization of artificial intelligence for our TSIA.
From a biological perspective, this dialog on engineering artificial intelligence has spoken extensively on the significance of Natures solution of evolving neural assemblies specializing in resolving the many varied invariances which the environment presents to an organism. And although fundamentally significant, the resolution of perceptual invariants cannot, by themselves, serve to build the more complex mechanisms which model the global behaviors of an environment that is generating those perceptions.
The “modeling” that is the product of these global behaviors cannot be developed by the neural assemblies performing the egocentric and allocentric abstractions characterized by invariance, because of a subtlety that has been totally missed by the collective AI community, and one that is not at first very easy to comprehend by the TSIA engineer.
Where those egocentric neural assemblies in mammalian brains accomplish their invariant derivation through an abstraction of time in a fixed spatial framework, and the allocentric neural centers accomplish their associations through an abstraction of that space in a fixed temporal framework, the higher order, global “sema-centric” neural centers accomplish global objectification through an abstraction of time in a framework of abstracted space.
And it is certainly forgivable if the TSIA engineer develops a (hopefully temporary) “deer-in-the-headlights” syndrome when trying to assimilate all of this.
So let’s start at the “bottom”, and as bottom-up engineers, understand from the very beginning that in every definition we care to look at, there will be dualities and circularities that cannot be contemplated separately. Now this perspective is what frightens mere academics into retreating back into hierarchical thinking, but as TSIA engineers, we will see that, in the mammalian brain, these behaviors of egocentric, allocentric and semacentric abstractions are being accomplished in each hemisphere of the brain, and that, in the brains of humans (and some species of apes), that differential between “right-brain thinking” and “left-brain thinking” (that has been alluded to in this discussion), is what reins in the dualities and circularities that result from all of these domain inversions being performed in each hemisphere.
Whew… Although the last paragraph was intended to clarify the discussion, the dialog must now throw in some additional bell-ringing wrinkles, because this biological characterization still does not provide a direct correlation to the logical implication-to-semantic inference-to-natural language reasoning process we are seeking to mechanize.
Unless we look at all of this from an even more “abstract” perspective.
Most AI researchers with a background in neurophysiology consider the functionalities expressed in the prefrontal lobe of mammalian brains to be the higher-level “global” center of neural processing. But the TSIA engineer should see that this perspective is borne from a gross mischaracterization that has been unfortunately propagated throughout the AI community, probably aided by those without research foundations in neurophysiology, a mischaracterization that espouses that the mammalian brain has a singular prefrontal lobe.
Knowing this, seeing that both hemispheres in the mammalian brain possess a prefrontal lobe, the TSIA engineer will also see that the egocentric, allocentric and semacentric functionalities of organic adaptation are all being performed in the occipital, parietal, temporal and frontal lobes of both hemispheres.
Given this perspective, human brain functionality requires a change in the conventional characterization of higher-order processes, because there are actually twin frontal lobe processes occurring in the brains of mammals, one in each hemisphere of the brain, so it would be incorrect to ascribe prefrontal lobe behavior as the “highest-order” center of functionality.
Certainly, if we were to indulge in some hierarchical thinking, prefrontal lobe functionality is of some “higher” order than the functionalities in the other three lobes, given that its treatment of the two domains of time and space are both abstracted, but the TSIA engineer should come to formalize the conceptualization that there is an even higher-order functionality in the human brain, unique in its product of catalyzing those emergent behaviors which give rise to intelligence in our species.
If we look at the two “lower” order processes of egocentric and allocentric apprehension in the mammalian sensorium, in this subjective experience, the world is presented to us as a set of objects that occupy space and have a variety of properties and relationships which result in sensory experiences of all sorts. Objects can be seen, felt, smelled and bumped into.
There is a learned relation between our non-contact visual perceptions of their form and location, and our tactile and kinesthetic perceptions when we touch or trip over them. Since we have no subjective sense of this process by which the cohesive impression of “objects”, as physical unified things, are built up out of the differentiations in multiple sensory modalities and our past experiences, this multi-modal, pre-conscious synthesis is presented to us as an accomplished fact, but it is really the product of a variety of activities occurring at all “order levels” of the brain.
However, we humans possess a unique multi-modal capability that is not shared among all mammals. The type of information transferred between sense modalities in human multi-modal synthesis is not the same as with all species. The ability to transfer information from one modality to another in a temporally modulated way is apparently well developed in only the highest of mammalian brains. Humans have no difficulty viewing a set of objects with the eyes only, and then picking out one by touch only, or vice-versa. Apes can also perform well on this task. Monkeys, however, have great difficulty with this and can do so only under special circumstances where the objects are of extreme relevance to the animal. Lower mammals cannot do it all, except in the case of very simple stimuli.
The physical basis for this ability appears to be the degree of interconnection between the cortical secondary sensory areas of the modalities involved, and also in some unique interlobe connections, (called fasciculi), between lobes of the mammalian brain hemispheres. In humans, there are large, well developed fiber bundles which interconnect the various secondary sensory processing around the occipital, parietal and temporal lobes. Among lower animals, only the apes have similarly developed connections.
And also in humans, this unique, richer multi-modal information transfer can be temporally modulated (allowing humans to see an object at one point in time and identify it by touch at another point in time). But this modulation requires a modulator, outside of the primary and secondary sensory areas.
Now, once this apparent “identification of equivalences” between objects, as perceived by the various sensory modalities, has been accomplished, the way is cleared for further perceptual analysis to proceed in a non-modality specific fashion, given this external modulation.
The modulator can then operate upon any perceptual information obtained about an object through the perceptual apparatus of any of the individual modalities, and the results of such processing can be added to a single set of “codes” for object qualities, which are now all part of a common, temporal and spatial set representing the unified object, regardless of the modality of origin.
And the physiological basis for that higher level “modulator” can be seen as the behavioral difference between the two hemispheres of the human brain, neurologically represented by the corpus callosum: That modulation is accomplished by the predilection of one hemisphere to form localized objectifications, which complements the predilection of the opposite hemisphere to form global invariances in the backgrounds to those objectifications.
This provides for the sort of perceptual analysis which occurs beyond the senses, because, in addition to the recognition of unified objects as such, their relation to the perceiver in space is known, through their multi-modal equivalences, and this analysis is imperative to all “higher” processes involving rational interactions with the environment, specifically for the temporally abstract “planning” of movement, in addition to those interactions that require the recall of information not specific to a sensory object or its position in space.
Especially the recall of object non-specific information, which means, in other words, the recall of a much smaller subset of all of the experiential knowledge of the agent which is relevant to this particular episode in its experience. A subset of the non-specific information which forms the ingredients for that elusive “modeling” behavior that the TSIA engineer should be starting to focus on.
At this point, it is important for the TSIA engineer to understand that this perceptual analysis, occurring beyond the immediate senses, which provides the “framework” for the intellect to gather other relevant “tidbits” of prior experiential knowledge in order to form a cognitive “modeling” product (in a temporally abstract way), would not be possible if Nature had originally produced a cognitive process which had to recall all prior experiential knowledge to form the perceptual analysis to begin with.
But that is precisely what conventional AI paradigms attempt to accomplish when using pre-abstracted objects and their predicates as the basis in their “reasoning” (or “learning”) models.
Now, there is a distinct facet of this intermodal equivalence, which leads to this unique extra-sensory perceptual analysis in humans, and that is the equation of words (the auditory objects of our “internal speech”), with objects seen or felt. (The TSIA engineer must keep in mind the fundamental concepts which distinguish between speech and language in this conceptualization).
The central area of the parietal cortex, which is bounded by the secondary perceptual cortex of the three spatial modalities (visual, auditory and tactile), is ideally situated to receive the necessary (temporal or spatial) location-analytic and object-analytic information of multi-modal perceptual analysis in its preprocessed form, (and in fact, each hemisphere has its own confluence area), but in humans, there are unique fasciculi that weaves linguistic auditory objects, (recalled as the subset of past experiential knowledge, the relevant “tidbits” just mentioned), into this perceptual analysis forming the basis for our temporal and spatial “modeling” .
The correlation between touch and vision is every bit as much a learned phenomenon as is this relation between word (auditory object) and visual or tactile objects. A great deal of time in the infancy of humans is spent in learning the relationships between touch and vision, and a great deal of adolescence is spent in learning the relation between words (speech) and that learned “fundamental logic” of things in the world, (the synthesis of logic and language that Marvin Minsky spoke of).
It seems that the ability to use symbols (in the form of rough auditory objects) at the level of perception where we perform intermodal associations is unique to humans, and to some extent, apes, because of this well-developed ability for intermodal object recognition in general.
And recall that this “lower-level” intermodal association and perceptual analysis is being performed with senses possessing multi-dimensionality in their signaling. Establishing “cooperative mappings” in this intermodal process plays a critical role in more conceptual processes. Analogies are understood by creating correspondences between elements from two conceptual domains, but there must be a common representation, a common mapping, between those domains. Indeed, at the core of analogical thinking lies the essential process of mapping: The construction of orderly correspondences between the elements of a source analog and those of a target. And in “higher-level” analogical reasoning, global consistency constrains the mappings that are created.
Certainly, this adaptive mapping activity is coupled to the ability of the neo-cortex in mammals as a whole to express a wide “dynamic range” in the dimensionality of neural maps and their processing, an ability having the capacity for fine distinctions and discriminations in some areas, and large-scale generalizations in other areas.
The world-related perception of experience is constrained, or constituted, in consciousness, and although experientially consistent, it involves the continual processing of inconsistencies. But how does all of this organic behavior help the TSIA engineer in the implementation of symbolically defined logic systems which can lead to semantic inference, and ultimately to natural language reasoning?
The highest level of satisfaction that a linguist can reach is the specification of a formal system that has universals as consequences.
This seems in opposition to a logical theory, which structures the process where particulars are derived from universals as consequences.
All of the issues previously discussed in every axiomatic logic spring from the (non-temporal) syntactic departures taken for the interpretation of the logic, and perhaps this can all be resolved when our logic system can correctly and formally separate the predication for any existence in a dynamic world from the predicates representing any changing relations among existences. But the only way to explicate the predication for existence in a symbolic logic, representing a dynamic world, is to introduce temporality into the very symbols of that logic itself, and not by any axiomatic device.
And this can only be accomplished while the TSIA engineer contemplates the actual mechanization of these processes, which is the subject of the next chapter in the dialog.