The Enterprise of Knowledge
In order to fully develop the necessary concepts to build the Ternary Logic required by the engineering of the Organon Sutra, we must initially look to the “enterprise of knowledge” that human reasoning systems have been engaged in, and see where the insufficiencies in these systems currently resides.

In his statement, De Morgan was surely referring to the application of logic, as a tool, to the reasoning process of the many persons of his time.
In generalizing a distinction between logical thought, and the expression of that logical thought, De Morgan may have provided 20th and 21st century technologists with the first clues to mechanizing that reasoning process and automating the application of the logic he was referring to.
Many academics contend that there seems to be two different conventions involved in reasoning – one is that of natural language and the other that of syllogistic logic.
We often reason based on the ground rules of natural language and practical considerations rather than reasoning via the laws of logic. The way we reason in everyday conversation is sometimes called natural logic, pragmatic reasoning or common logic.
Indeed, the science of logic has set out to provide us with a sound theory of reasoning, to insulate us from the tendencies of natural reasoning, but much of the time our ability to reason logically is hampered by language.
Within our usage of everyday language, the meanings of words depend on a whole host of factors. We automatically take context into consideration to understand each other and only become aware of context when something goes awry and our communications breaks down (the implicit context becomes explicit).
In the process of human reasoning, we do make reasoning errors. It has been suggested that these errors arise mainly from reasoning from wrong principles rather than wrong reasoning, in other words from the matter being reasoned about, rather than the form of thought.
Sometimes we “reason logically” from wrong premises and sometimes we fail to use sound judgments when forming the basis for our premises. And there seems to be a fundamental difference in the very processes used between formal logic and common sense logic.
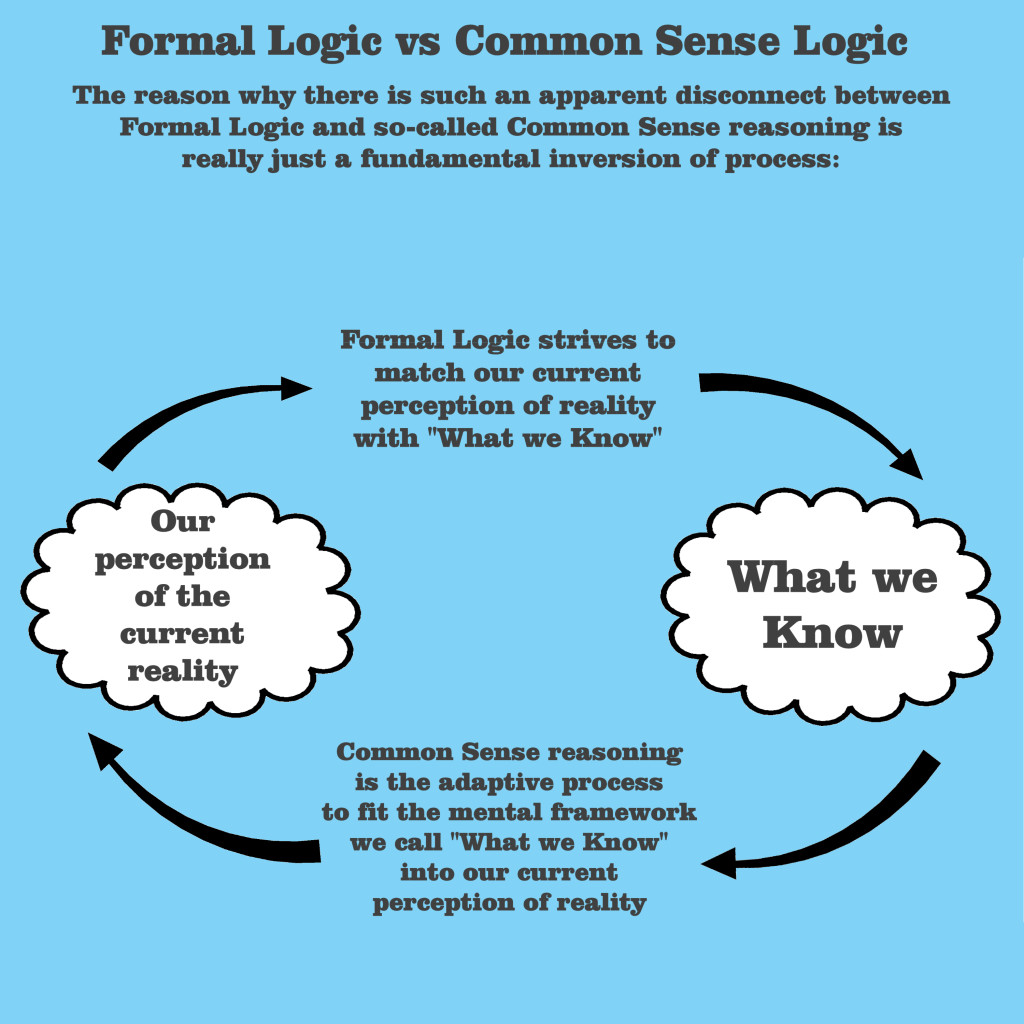
When fashioning our mental approach in the reasoning process, we tend to select what we believe to be relevant information, not all information. People consider the most plausible model rather than all possible models when framing the reasoning process.
Also, the ambiguity of predication and relation (the difference between “is”, and “is a”) in logical expressions can easily lead to faulty reasoning. The predicates of classical, propositional and first-order predicate logics necessarily conflate the expression of existence with the expression of relation. This results in an ontological dilemma – how can a logic system predicate the relation of things using the very predicate which expresses their existence?
And, as history demonstrates, when you get right down to it, as the now famous Bill Clinton defense goes, “it all depends on what the meaning of ‘is‘, is”.
Our language also makes it possible to construct formal logic paradoxes, or logical situations that seem contradictory in nature (the most insidious paradoxes involve claims that reference themselves, the so called autological assertions. The liars paradox is the most famous of these).
In time, the discrete logics of class inclusion and set truth (encompassing the propositional and predicate logics) were supplanted with the fuzzy logics and multi-valued logics of assigning partial truths, that attempted reasoning outside of (nominal and ordinal) categorical contexts (gray area reasoning).
The need for probabilistic logics and temporal logics demonstrated that a great linguistic gulf still existed between common reasoning and the formal processes, although no formal logic seemed capable of spanning that gulf.
Where the formal logic referred to by De Morgan was a tool to discipline the processes of human reasoning, a systematic which would allow a machine to employ a form of automated reasoning would, from its very foundations, necessarily have to reconcile the two following constraints:
1) In common logic and ordinary conversation, we assume a great deal of background and cultural knowledge when we argue or explain. We have a great many unspoken assumptions about how we will be understood. Everyday reasoning utilizes all of the information at the reasoners’ disposal.
2) Formal logics require the reasoner to make all information explicit, with no implied knowledge in meanings, and only the minimum commitment entailed by the premises must be accepted. Formal logic reasoning requires that only those conclusions that follow from the premises be accepted.
In visualizing the form this mechanical reasoning process would take, we would first want to reconcile the concepts of common logic with that of the disciplined formal logics.
During that visualization, as the concepts emerge which reconcile the common with the formal, we must also begin a program to move from words (implicit ideas) to symbols (explicit ideas), and from reasoning (common logic) to inference (logical chains of assertion).
At first, it seems that it is only in the realm of symbolic logic and goal driven inference that we can hope to mechanize some useful form of natural reasoning.
Unfortunately, our symbolic tools do not possess the sophistication to mechanize the entirety of our “natural reasoning”, even if we were able to define and generalize all of the nuances of our language.
And it is naïve to believe that we can fully abstract our words to derive only their basic explicit symbols. There will always remain some implicit understanding in our symbology that cannot be generalized, which will “distract” the mechanical reasoning process.
As this dialog will not concern itself with the philosophical considerations of whether computer programs will ever possess the ability to mimic human natural reasoning, we will explore the potential for an artificial agent to exhibit behaviors which might allow it to rationalize the infinity which it perceives.
The formal logic of Augustus De Morgan works well in helping the people he spoke about to discipline the application and expression of their reasoning process, but it is not fundamentally suited to creating syntactic systems for machine execution which might demonstrate an artificial reasoning facility.
If our desire is to automate just the most basic reasoning mechanisms (reasoning as in the application of logic principles and inference rules to move from a universe of evidence to a focused conclusion), then much of the principles of formal predicate logic can be retained. But the automation of a reasoning process that can apply mechanical processes to an open-ended Universe of Discourse, will require the resolution of a fundamental ambiguity encountered when mechanizing those aspects of logical process, an ambiguity which is implicit in all human logics of discourse.
In human logics, there arises an implied ambiguity of existence when referring to an entity, in that the discourse implies the existence of an entity whenever any reference is made to it. Within the binary definition of boolean logic, this flaw is inherent in boolean systems, but even in the realm of classical logic, this ambiguity of assertion remains. At the most fundamental level then, to resolve the “ambiguity of assertion” and many other issues besides those of existential import, (such as the inability of the predicate logics’ to deal with expressions of change or express temporal concepts), the infinite logic systematic will introduce the formalized definition of assertion.
Where the formal logics deal with assertion as solely a semantic grammatical aspect of propositions, an intelligent systematic will define assertion as an intrinsic property in propositions.
To do this, the systematic introduces a definition for a 3-state logic valuation, called Ternary Logic, which demonstrates how these new concepts of valuation will eliminate many of the ambiguities and quandaries which have bedeviled the application of formal predicate logic to all areas of common reasoning discourse.
But just replacing the truth rules of binary logic with a ternary truth definition is not sufficient to accomplish this. A ternary truth definition cannot be derived superficially. For this, the systematic will visit those most fundamental concepts of formal logic, the three classical Laws of Thought, to see how, with a slight restatement, the new concepts of Assertion and Ternary Logic can be melded in to the classic definitions of a predicate logic definition to form the basis for a mechanized reasoning system.
The basis of the Ternary Logic definition
The purpose of the Ternary Logic definition is to provide the rules for assigning a logic “value” to any proposition or logical statement in a system of infinite logic.
One of the prime requirements of the Ternary Logic definition is the separation of any logical reference to a “thing” from the implication that the “thing” exists, the so-called ambiguity of assertion. Existence should be an explicit property of something.
To see the distinction between the two concepts, use this generalization:
Whenever we are talking about a “thing” in terms of “is-a”, then we are just making a reference to the “thing”.
Whenever we are talking about a “thing” in terms of “is”, then we are asserting something of that “thing”.
Every logical proposition in the Ternary Logic definition can be divided into one or the other generalizations. This is a very key distinction in the Ternary Logic definition, and must be kept in mind. In many formal logics, the distinction is not always explicit, and therefore ambiguities become prevalent.
In the principles of an infinite logic, a “thing” is called a Referent. And, in concert with those principles, we outline the logical property of Assertion, which is more specifically defined as a property of Referents.
Now, to have any utility in a reasoning system, the Ternary Logic interpretation must represent its logical “valuations” in a manner which is reconciled with the fundamental, classical “Laws of Thought”.
Because, if we want to be more precise about our definition, we will find that the classical Laws of Thought and the Principles of Ternary Logic cannot be addressed separately, and we discover that it is the classical Laws of Thought which define what semantic “logic value” is, at which time we understand that the Ternary Logic establishes the syntactic rules for assigning those logical values to our propositions.
In formal logic systems based on a binary logic definition, the entire discussion was fairly simple.
The classical Laws of Thought, through their expression of dichotomy, defined two valuations, which were TRUE, and NOT TRUE. (As the discourse on logics progressed through the ages, the valuation of “not true” was later given the alias FALSE, which is unfortunate, because it clouded the spirit of dichotomy and the concept of “is” and “is not”, and the role of the Laws of Thought began to lose their classical place in logic “definition”).
So, with these two logic valuations, the assignment of value was straightforward: a logical term was either True, or it was Not True.
And in many areas of life, simpler is better. But unfortunately, in so many areas of human discourse, this simplicity was found to be insufficient, and introduced ambiguities. And the most pronounced insufficiency of the binary logic definition became apparent when logical statements were created to express concepts of change. In order to avoid these binary logic constrictions, the development of a mechanical reasoning systematic determined that a minimally sufficient logic definition requires at least three valuations.

The proposed “ternary” logic values are shown in red. But, as has been stated, logic valuations spring from the classical Laws of Thought, so any “additional” logic valuation beyond the previous binary values must come from there. If we do not perform our due diligence, then even more fundamental contradictions and inconsistencies will undermine any expanded definition of valuation.
When we are referring to the most fundamental basis of the formal logics, there is nothing more fundamental than the three Classical Laws of Thought:
– The Law of Identity
– The Law of Non-Contradiction
– The Law of the Excluded Middle
In order to properly incorporate our newly devised concepts of Assertion and Ternary Logic into a reasoning framework, it is necessary that we assess their participation in these fundamental Laws.
Initially, with all due respect to Aristotle, the first pitfall in classical logic is that when a reference is made to a “thing” in a proposition, there is also an implication made that it exists (implied existence). This creates problems of Existential Import in traditional logic, which the Ternary Logic eliminates.
In human discourse, we employ a capability to reference hypothetical “things”, which may not exist at the time of the discourse. For instance, our language allows us to discuss “a plant living and growing”. Implicit in that discussion and implied in the language is the plant state “before living”. There is an implied state of non-existence of the plant, which our language allows us to freely use in implications of this sort.
As many states of change and temporal concepts occur throughout our everyday lives, our language is rich with devices to express these concepts, but expressing things like change and temporal relations becomes cumbersome and inelegant in formal predicate logics with a binary logic valuation.
The very genesis of tertiary logic state definitions was to alleviate these constraints in the formal logics, and allow a more “natural” mode of expressing these concepts in the predicate logics.
So, beginning with the Law of Identity, which states that an entity can only “be” that entity, that it cannot also “be something else”, we find that with a Ternary Logic description, the Law still holds its axiomatic reign in the fundamentals, and requires only a peripheral redefinition.
When we include a definition of Ternary Logic in our conceptualization, the Law of Identity still stands, for when we assert an entity to “be something”, it cannot “be something else”. This is, in essence, the concept of dichotomy, which the Law makes explicit.
And if we interpret the Law for an entity in the tertiary state of not existing, (the ternary value of unknown, or more formally, not asserted), then there is no definition for that entity “being” in any state whatsoever, so the Law is satisfied.
The Ternary Logic definition allows us to make distinctions between the reference to an entity (“is-a” statements), and any existence of an entity (“is” statements). This is necessary to allay that first and most difficult issue with classical logics (reference implies existence).
The Ternary Logic allows us to fully define an entity (“define” meaning placing it in a classification relative to the context of discussion) by making references to it, without asserting existence.
“Existence” then becomes a formal predicate, and asserting existence becomes an intrinsic property of an entity, separate from its definition (which would be all references to it).
An existence predicate now opens up a mechanism for all of the expressions of change and temporal concepts which have been so difficult previously. We can now discuss an entity that doesn’t exist in any manner that we wish, and we do not need to resort to such futile “tricks” as allowing something to be both “true” and “false” (as in the Dialetheism proponents), in order to force our logic system to express concepts of change.
Although the Ternary Logic does not formally define what “being asserted” actually means at this point (the formal definition occurs outside of the Principles of Ternary Logic at the level of ontologic entailment), it can be said here that the doctrine of assertion is the fundamental mechanism employed by the systematic to make explicit the difference between “is”, and “is a” (all “is a” propositions are non-assertive, or merely references, where all “is” propositions are assertions).
In our analysis of the fundamental Laws of Thought, we will jump to the third law, the Law of the Excluded Middle, which states that for any proposition, either that proposition is true, or its negation is true.
In order to reconcile the principles of assertion and Ternary Logic with the Law of the Excluded Middle, we re-state it in terms of the two levels of definition in the Ternary Logic. And though the re-statement comes in two parts, for the sake of comprehension we will begin with the first part:
Given any proposition, either that proposition is asserted, or it is not asserted.
This declaration is first interpreted in light of another fundamental premise of logic systems – Logics are usually systems intended for preserving some semantic property of propositions across transformations.
In classical logic, this semantic property is simply the property of truth.
Under the Principles of Ternary Logic, there are two properties for which we apply this “preservation”. The first property is the property of assertion. So the first part of the re-statement is required to include the assertion property within the re-definition of the Law of the Excluded Middle, and now the re-statement declares that a proposition may either be asserted, or not asserted, and that there is no “middle ground” or third case in which we can interpret it.
The second property for which we will apply the Law to, is of course, the classical values of True, and Not True. With these, we have the complete re-statement of the Law of the Excluded Middle:
Given any proposition, either that proposition is asserted, or it is not asserted. If asserted, that proposition is either True, or its negation is True. If not asserted, that proposition is Unknown.
With this re-statement, the Law of the Excluded Middle gives valuation to the three ternary “values” of truth in the Ternary Logic.
While we are here, it is important to emphasize that “asserted” and “not asserted” are not logic (truth) values. They are properties of Referents and propositions. “True”, “Not True”, and “Unknown” are logic truth values.
The Principles of Ternary Logic outline the rules in which we arrive at one of the three valuations when considering any proposition.
With this, the Principles of Ternary Logic considers (the re-statement of) the Law of the Excluded Middle to complete the second dis-ambiguation of dichotomy created by the Law of Identity (the Law of Identity creates a dichotomy, wherein the two parts are mutually exclusive, and jointly exhaustive. In completing the second dis-ambiguation of dichotomy, it is an expression of the jointly exhaustive closure).
We conclude our analysis of the fundamental Laws of Thought by considering the second Law of Non-Contradiction, which states that contradictory statements cannot both be True, and Not True in the same sense at the same time.
The Law completes the first dis-ambiguation of dichotomy created by the Law of Identity by declaring dichotomous concepts are mutually exclusive.
However, it is this Law that has been the most difficult to resolve when classical binomial logic has been employed to express temporal concepts, and especially in expressing concepts of change.
In classical logic, the application of the Law runs into difficulty when the context of a proposition extends beyond that of logical being (a thing “is”), e.g. when the logical context includes statements regarding change or time.
When we say that a thing “changes”, we are saying that, at this time a thing “is this”, and at another time, the thing is “not this”, which is so difficult to express with the limited binary logic valuations.
It is in the re-statement of the Law of Non-Contradiction that we see the real utility of the Ternary Logic system emerge. The re-statement is straightforward:
Two propositions, both having identical assertions with the other, cannot both be True and Not True.
Note that there is no conditional “in the same sense”, as this is made explicit by the assertion properties of the Referents participating in the statements.
And, there is no muddying of the logical waters with any murky reference to TIME. “Time” is a concept that MUST be left to definition in the Universe of Discourse, and not chiseled into the granite of fundamental law.
So, with this re-statement, we can place that most compelling concept, Time, back to where it belongs, in the Universe of Discourse, and our (re-statement of the) Law of Non-Contradiction is now in its cleaner, simpler form.
The Principles of Ternary Logic emerge from a position of pragmatism, only more narrowly defined, in that the function of machine inference is to provide a basis for machine reasoning and problem solving.
In most formal logics, the Universe of Discourse is agreed upon before-hand, and then brought to the table, at which time discussion and reasoning commences.
With the concept of the “property of assertion” being a composite element of the Ternary Logic, the reasoning mechanism which expresses it is now able to participate in the definition of the very Universe of Discourse itself.
This is a very important distinction, and it is essential to any future systematic that strives to express any capability of machine inferencing.
Although it is very subtle, and not readily apparent, it is this participation in building the very Universe of Discourse that a machine systematic will “reason” about, that allows that systematic to claim to possess “knowledge” in its reasoning.
This is the true power of the Ternary Logic.
Freed from the prejudice that occurs when the concept of time is inscribed into the fundamental Laws of Thought, a machine inferencing systematic can now build any concepts of change into the Universe of Discourse as it will, with none of the previous contradictions of a limited binary definition.
The Ternary Logic Operators
The preceding sections outlined the definition of the ternary state representations for the Logic of Infinity in the Organon Sutra artificial intelligence systematic.
Following the definition of the ternary states, an infinite logic needs to define the logical operators which express the syntactic behavior of these three state representations.
It is at this point that most definitions of tertiary logics begin their description, or at the very least, specify a representation of their values, such as -1, 0, 1 or 0, 1, 2.
Yet these symbolic aliases provide only a superficial treatment of the inherent ambiguities that arise from a formal system based on binomial definition, and do not formalize the foundational semantics of trinomial assertion.
Because they do not reconcile their tertiary forms with the bivalent principles of the fundamental Laws of Thought, their systematics are difficult to embrace, and their definitions have not garnered any significant acceptance. (Although, as a note, the infinite logic of the Organon Sutra will adapt one aspect of conventional binomial and tertiary logics. For the duration, the definition will utilize the alias “FALSE” for the prior labeled state “NOT TRUE”, in order to maintain some conformity.)
There are several major considerations in any three-valued syntax. Without regard to syntax, there are 19,683 (3^9) unique permutations to a two-variable argument function of the trivalent case.
Beyond the fact that such a huge number of functional products would define a logically meaningless system, there must be some ontologic semantic that defines a minimal set of the possible permutations which can construct useful operations that express the conditional properties of assertion, such as commutativity, associativity, reflexivity, idempotence and distributivity.
Boolean set theory has established a number of common constructs, eliminating all of the two-variable operations with products that are independent of one of the variables, but a three-valued logic introduces new considerations.
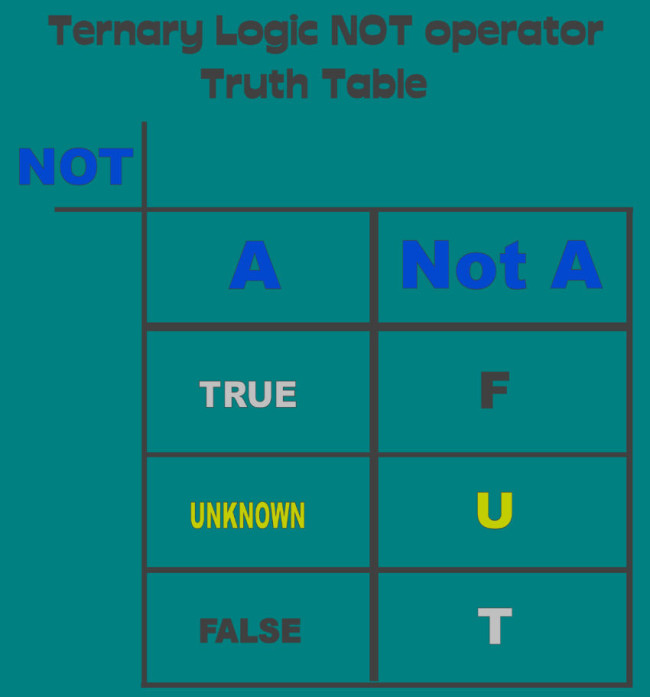
First to be considered would be the unary operators in a three-valued logic. The semantics of boolean set theory constrains to a single unary operator, which has the alias NOT. However, the assertion semantics of the Ternary Logic requires a revised syntactic behavior of the NOT operator (producing identity on the UNKNOWN input), and this semantic also requires an additional unary operator, analogous to the NOT operator, called the Unasserted operator, (having the alias NOTA), which returns TRUE if the input is unknown, and FALSE otherwise.
A third unary operator, which would produce the functionality for state inversion, is not as trivial in a three-valued logic as it is with a binary system. For instance, the inversion of TRUE might intuitively be FALSE, but what is the inversion of UNKNOWN, is it TRUE or FALSE? Certainly, inversions are most useful when they are reversible, but the design of the Ternary Logic will punt on this unary operator, and consider logic inversion to be a semantic entailment, with no syntactic intuivity.
Also, the implications of a three-valued logic become ever more complicated if considered as a generalization of a binary logic. In any framework for reasoning, a semantics defines meaning and truth, and a syntactics preserves truth across reasoning transformations. In the semantics of the Logic of Infinity, meaning and truth hold intertwined identities under ontologic entailment and assertion. This duality of identity cannot be accomplished with a closed semantic system of axiomatics composed of non-dimensional symbols, but can only come about from a system based on active, temporally dimensional components, as defined by the Aperions of the infinite logic. Truth is no longer a static mapping among syntactic operators. Truth is a property among entities that have an active, dynamic history of assertion in their definition.
But the functional nature of axiomatic logic should also be retained in the active systematic of the Ternary Logic, and this functional nature is expressed as those modal operations which can construct semantic propositions, which form the grammar of logical transformations. (Because of the dual identity of entailment and assertion, the semantic propositions of the logic of infinity have a dual capacity to define logical objects themselves, in addition to mapping their truth value across transformations.)
In embracing the functional nature of axiomatic logics, the Ternary Logic retains the modal unary operations of Identity (or Affirmation), Denial (or unary negation), Tautology (if X, then X), and Contradiction (it is not true that if X, then X), along with the modal constructive operators of Conjunction (AND), Disjunction (OR), Implication and Equivalence.
However, under a three-valued logic, Implication in this consideration cannot be derived from the three basic operators of Negation, Disjunction and Conjunction as it can in a binary logic, and the extension of a three-valued logic into a boolean algebra, comprised of the axiomatics of boolean set theory (with its axiomatic definition of a Power Set and the Null Set), cannot reconcile the contructive tautology which produces the boolean definition of a Power Set, or the constructive contradiction which produces the boolean definition of the Null Set.
Although the set of static logic tables would be the final product in a Ternary Logic definition, the logic of infinity as defined within the Organon Sutra merely starts with these syntactic modal operators, because the active nature of the infinite logic must now take into consideration that one faculty which has been absent from every 20th century logic – the semantic enterprise of creating the very objects a logic system will submit to its syntactic machinery.
And the logic of infinity must demonstrate the very paradoxical behavior of creating those logical objects from that syntactic machinery. 20th century logicians missed the critical ingredients emergent in the unique 21st century Logic of Infinity, which now provides a framework for the true mechanization of reasoning by an artificial intelligent agent.
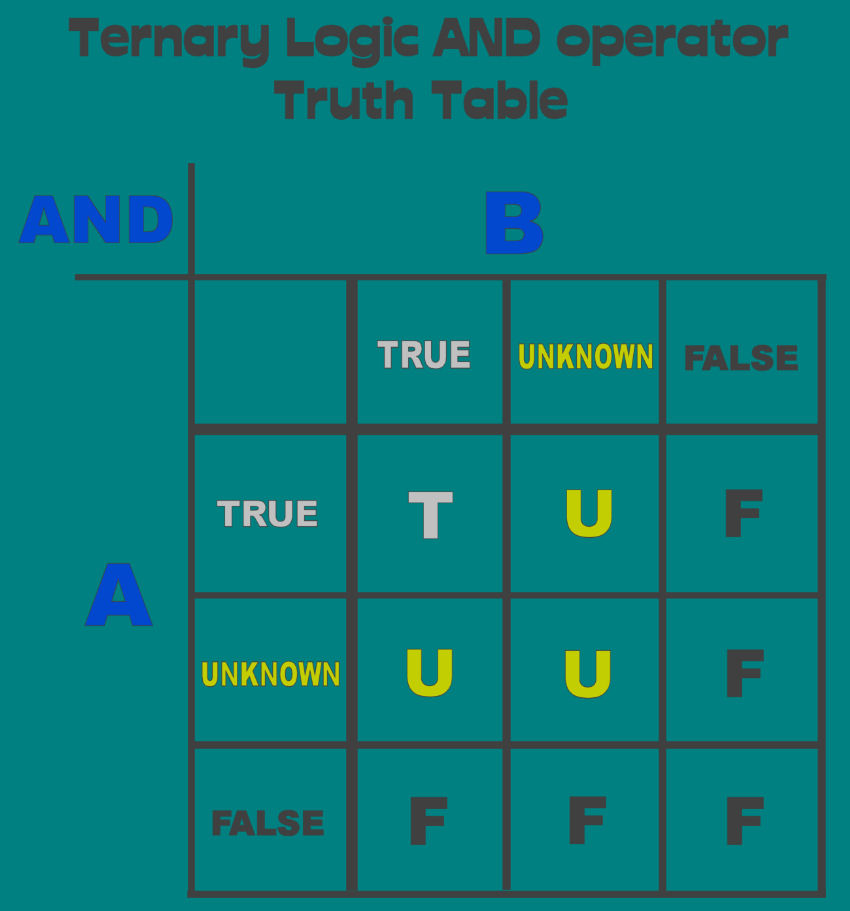
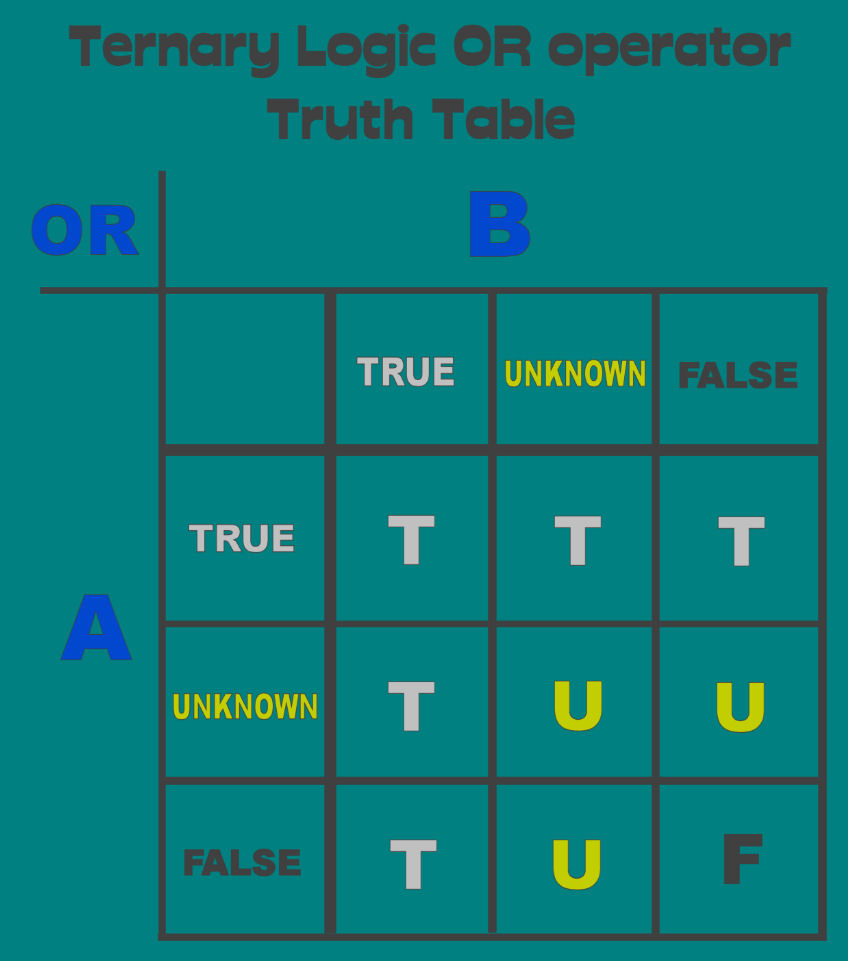
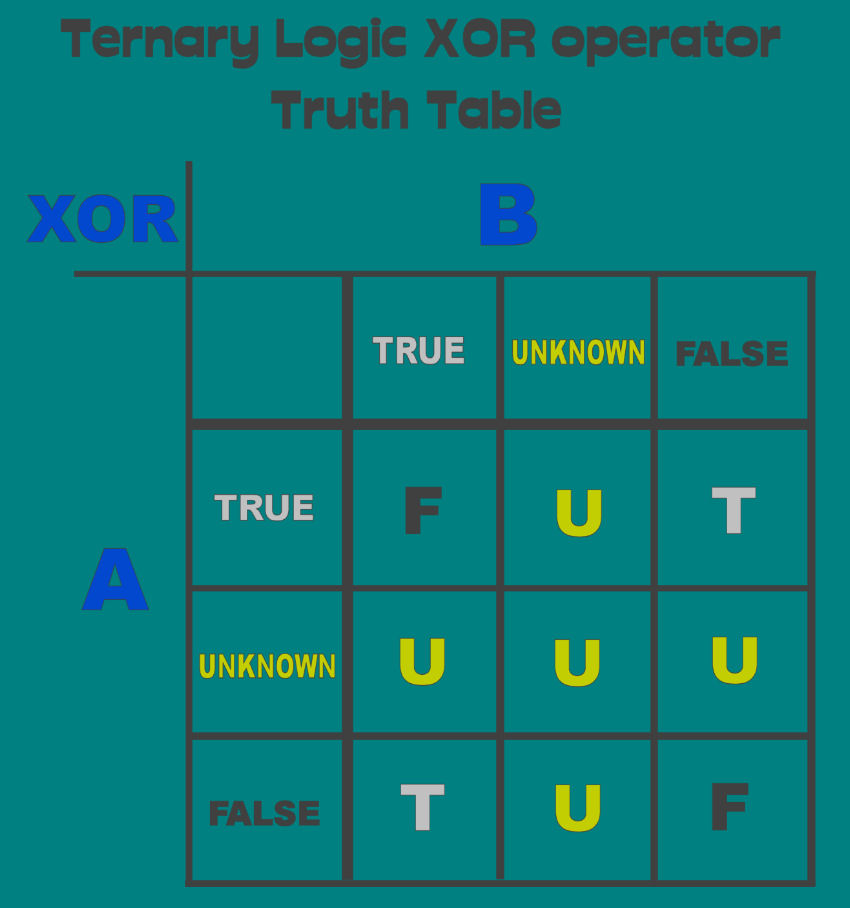
Shown next is a representation of some of the static Ternary Logic truth tables.
The Logical AND Operator
The Logical OR Operator
The Logical Exclusive-OR Operator
The Logical NOT Operator
Go to Intelligent Logic Inferencing Systems
Go to Top of Page
Copyright © 2020 All rights reserved