The Machine Implementation

The machine within the machine, and the genesis of all digital representations, which requires a complete transformation in digital programming
Imagine the challenge of putting together a picture puzzle whose pieces intermittently change shape, and which have a shifting superimposed image which rarely remains the same, and you can begin to see the challenge that Nature faced in evolving a neural organism that could master the cognitive abilities to model the world outside of it. Because the external world is constantly changing, “things” move in relation to one another and also morph over time.
Although we left off with a discussion on semantic inference and logical implication, a digital implementation of the intelligent behaviors in our engineered TSIA will not actually begin with a mechanization of inference and implication, because to do this we must first resolve the differences in any machine design based on a connectionist approach versus a symbolic approach.
From the very start, the top level mechanisms in any TSIA must create an intentional process, which systematically builds a model of the “outside world” into the “inside” of the machine that will be conducting this adaptive inference and reasoning. This systematic execution occurs through the directed movement from current internal states to target internal states, which in their genesis, must reflect certain core design principles of the TSIA engineer. However, this “state machine” must differ in a significant respect from most other conventional state machines.
The TSIA state machine cannot be defined by a closed set of machine states, with any current state having complete determination of subsequent states by virtue of a closed state transition function.
But certainly, a random state transition function would not be workable, so the variety of new state transitions in this “open state” machine must follow the modeling process being reflected in any intentional reasoning facility, while they simultaneously build that very model. Yikes! More duality…
And yet, even at this very early stage in the definition, before a more concise determination can be provided on the particulars of a mechanization of this “modeling” process, a clearer conceptualization of these internal states in the engineered TSIA must be brought about, in order to provide a foundation with which to orchestrate the execution of their transitions.
(For purposes of this discussion, these top level mechanisms and internal states will be collectively referred to as the TSIA Executive).
Now, from a hardware perspective, implementing any “reasoning system” in a digital form using the classic Von Neumann computer architecture creates a number of conceptual bottlenecks. And the most crucial of those involves the concept of latency.
Executing a programmed “reasoning system” on a digital processing system with a single accumulator per clock cycle (the definition of a Von Neumann computer), is like moving the water out of a bucket with an eyedropper. It is possible, but there are certain external events to the processing system that possess a temporal latency for which the “eyedropper” must keep up with. In this (very coarse) analogy, the eyedropper must over time remove at least as much water from the bucket as any new water dripping into it.
However, starting with a Von Neumann architecture does have a few positive advantages. Besides having a huge body of developed application history, a design intent that begins with that single accumulator in our implementation will prove to be the key to intelligent digital machines, in a way that will unfold as the dialog continues.
So if the implementation of a TSIA’s processes is to be realized in a digital form, then the architecture of the digital hardware must first address this temporal constraint of latency before any software programming of that hardware, and that subsequent software programming must then be designed in such a way that avoids the three most intractable constraints which have bedeviled every conventional computer program since the early 1950’s:
- The software related representation of structures and relationships explicitly.
- The hardware related segregation of “data” from its processing machinery.
- The virtual inability of discrete, non-dimensional binary structures to represent continuous time.
These three constraints have been at odds with computer programming goals from the very beginning of the digital era because they are very closely interrelated, which means that they are very difficult to address separately.
Top level translations from state to state in the engineered TSIA are defined by a fluid structural framework whose temporal characteristics must first resolve what is called the penalty for representing data structures and relationships explicitly.
But the resolution of this penalty is exacerbated by the hardware considerations of data storage, hardware considerations which complicate the necessary resolution to this penalty for explicit representations of structure, constraints that also overshadow the considerations of data usage, usage considerations which should be the primary focus of the traditional computer programmer.
Now, from the perspective of a digital TSIA’s processes, the ultimate consideration of programmed “TSIA” data usage must, at some point, be in the creation of binary techniques to synthetically represent continuous time. (In the case of today’s digital computer technology, most programmed applications can fortunately implement an abstracted representation of “time”, which can be symbolized as a non-dimensional concept). However, any useful representations of time in a synthetic intelligent reasoning system are made virtually impossible with the prevailing conventional attitudes toward digital “data”.
For sure, it is difficult from the very start to establish even a conceptual framework for “time”. Our very biological apprehension of time is variable. For instance, everyone has felt the effects of perceptual time on their individual experience of the world: When we humans are hyper-alert, there is an internal mechanism which shifts our internal measure of time progression. Because of this, there is that familiar effect that, when in a state of hyper-alertness, we “feel” that the external world is moving slower than usual. And surely everyone has experienced the dismaying sense of the clock slowing down while we are at work, only to sense it speed up during periods when we are enjoying things the most.
This demonstrates that our “biological time” is subjective. Our internal metering of the passage of time is measured by our apprehension of the external world, and not, as the academically inclined would have it, by the metronome of some “external clock”. The external world may for sure change to the beat of some external drum, but our “internal time-keeping” does not resemble that external time at all, and confusing the two would be an irreconcilable error in the design of our digital TSIA.
And even defining a useful representation of time in the binary language of ones and zeroes is difficult. This is perhaps evident when the TSIA engineer undertakes a definitive understanding of “time” itself, since, in a philosophical sense, there emerges a “paradox of time”, that becomes apparent when one realizes that “time” does not exist as a separate phenomenon independent of all other observed phenomenon, which means its representation becomes inextricably tied to the representations and changes in any observed phenomenon.
History recalls the very early lessons that seafarers learned when trying to determine their geographic position during transoceanic voyages. Once the sight of land disappeared beyond the horizon, everything in transoceanic navigation, from the estimation of speeds and distances, to the very calculation of position depended upon an accurate representation of time, not in absolute terms so much as the duration of time for each of the phenomenal aspects they were measuring.
Given this philosophical consideration, a more refined functional determination for binary representations of time reveals that the phenomenon of time cannot be separated, in abstraction, from those objectifications in a TSIA’s environment, and so the apparent “paradox of time” emerges when the TSIA engineer realizes that “time” by this definition cannot exist until an observed invariance exists in the perceptions of the TSIA, and that “time” cannot progress until any change to that observed invariance occurs, creating an engineering dilemma which should shape and fashion the entirety of any TSIA design from the very beginning.
And hence, a digital resolution to this paradox cannot come about until the historically omnipresent hardware and software constraints of digital data representation are resolved.
Although these hardware, software and virtual considerations are mutually antagonistic, their mitigation is typically addressed separately. This should prompt the TSIA engineer to begin with a more comprehensive approach, by learning the lessons of computer science history, which in retrospect demonstrates why these three constraints remain unresolved. Although the piecemeal approach to resolve these constraints has brought us the impressive world of digital computing we have today, separating their mitigation has also frustrated every historic effort by academia to make the clockworks of the traditional Von Neumann digital computer turn in some fashion that could be called “intelligent”.
Since these three fundamental issues have been historically addressed separately, even though they are inextricably intertwined and mutually antagonistic, the entire discipline of computer programming has been profoundly hobbled from the very beginning, as size restrictions on the storage of data, irrespective of any considerations in the representation and use of data, have required programmers to write code which manipulated the data after it was encoded for storage, greatly complicating the already complex task of computer programming in ways that have still yet to be brought to light.
When “data” is encoded for storage prior to the compilation of the code that will “process” it, the semantic implicit in the data elements themselves becomes enmeshed with the encoding scheme used for the storage of these elements, and then, when computer programs are composed apart from this encoding process, there is oftentimes a programming juggle between the significance of the storage structure of data, the semantics of their explicit representation, or the significance of certain relations between elements.
This juggling act has historically been a part of the traditional approach to computer programming, and at first the programming endeavor addressed just the singular penalty for representing structures explicitly, which can be introduced as follows: In designing computer applications, rarely does a computing task reduce to a simple list of data elements (operands) to be passed through a function process (operator) to produce a desired result (output).
In every computer application, the construction of the “functions”, which transform the “data”, must actually follow a dual, parallel production. Certainly, first to be considered, there is the machine implementation of the abstract transformation itself, but what is most times only given secondary attention is the algorithmic effects of the binary structure of the data as it is presented to the function code.
This means that the construction of abstract transformations is equally dependent on the digital structure of the data being transformed (where structure is an implied combination of representation + storage), and that to make use of any structures in data elements, the execution of defined function processes in a program (after its compilation) must have something explicit to “evaluate”, apart from the essential semantics of the data, which normally requires the creation or definition of a new data element to specifically represent the structure (the combined representation scheme plus the storage scheme).
For example, consider a simple list of words to be manipulated according to some algorithm. Even before focusing on the words themselves, a new “data” element representing the number of words in the list must be created, which means that the composition of the original data semantic begins to change. And although counting the words in a list is a trivial matter, establishing a concrete, explicit element to represent their numerosity incurs additional costs, such as data dependence and type specification constraints, local memory allocation and housekeeping costs, and these immediate costs are significantly compounded by future processing and storage obligations.
All of the algorithms which subsequently process this list must now also accommodate that specific structural “data” element. Changing the length of a list now involves updating all list processing functions, for example.
Unfortunately, in every programmed computer application, there is also a compromise which adds another wrinkle to the approach taken for data storage, which is itself irrespective of the considerations of storage limitations. At its most fundamental level, all “computer data” representations must acknowledge that there are two opposing intentions that must be decided beforehand when structuring data for storage in any digital computer architecture. On the one hand, data can be structured for optimized access by the algorithmic process which will be manipulating it, as in a list or a stack. At its extreme, this intention is expressed in the ubiquitous database architecture, where atomic data elements are individually structured by separate, predefined contexts, or keys.
Structures optimized for access might also be defined because there exists multiple code modules which require a pre-determined, common structure in the data, where the atomic definition of the data is implicit in the accessing code, structures which also further distance the data from the functions that process them.
On the other hand, this fundamental opposition in representations can structure “data” to be optimized for its transformation, in a representation that places additional significance on the relation between atomic elements, where their overall mapping is a virtual part of their transformation semantic, and where the data, once accessed, is transformed into a new semantic that may have entirely different storage dynamics.
These opposing memes in structuring data for storage get blurred, unfortunately, by the demands of programming language paradigms and the concrete realities in the physical form of digital storage, and this blurriness complicates a very unique aspect in programming for artificial intelligence designs. This unique aspect is important to the TSIA engineer for the reason that an artificial intelligence systematic in essence strives to create structures which form new knowledge from existing data. The data becomes the constructive agent when “code” is designed in a true artificial intelligence application. With the introduction of the concept of countably infinite structures in the Logic of Infinity, it is the “data” itself which should shape the “code” that is manipulating it. Yet this creates a circular demand that the derived code also derive new structures for its derived “data”.
In traditional computer programming, program construction typically occurs after the data (which the programmatic functions will process) has been structured for storage and manipulation. Those derivative structuring elements, derived as explicit representations of structure, are treated by code processes as “abstract” elements. In other words, their definition does not describe a specific thing, but defines a class of things, or a general form that many things have. In the previously mentioned word list, each word is a specific element representing a unique definition, and the definition for the length of the word list is an abstraction that should not represent a specific list, but should apply to all lists.
The Object Oriented Programming paradigm of constructing object type specifications in tandem with the structural considerations of their functional application was an attempt, in the right direction, to address the penalty for representing structures explicitly, however this methodology still required the “object” specification to be established prior to program runtime.
But what of those “objects” whose structural definition may not be encountered until after runtime? Since it is the intention of the TSIA engineer to design a TSIA Executive which can form uniquely new knowledge structures from existing “data”, what of the penalty for those as-yet unknown structure representations?
This post-runtime representation penalty is termed “structural entropy” in the lexicon of the Logic of Infinity, and so, before we can even begin to speak of the systems which derive any new knowledge, the mechanisms of the TSIA Executive must be capable of producing new derivative structures from existing data in real-time which reflect the (structural) entropic cycles of its particular environment, in addition to accommodating the manifold issues surrounding the penalty for explicitly representing structure in any new transformation.
To do this, the architecture of the TSIA Executive must formalize an essential distinction at the design level between the very forms that “data” can express, indeed the very definition of “the experience of data”, a distinction which formally distinguishes between “data” as being either static semantic symbology, or “data” as being (time) dynamic signaling. And this means that now, because of this distinction, our conceptualizations of ‘storage’ and ‘memory’ must also change in a very significant and fundamental manner.
Where contemporary computer programming begins with a regime of pre-structured “data” in predetermined physical and virtual forms, artificial intelligence programming in the digital realm must have a design intention which begins at the point where an entirely novel data semantic is created by some transformation, because this design intention is also, simultaneously, the creative agent for that transformation.
The distinct structural forms that resolve from a dichotomous definition of “data”, (as being either static symbology or dynamic signaling), presently changes our definition of data storage, which in the new sense now defines a specific relation, one that also has a dual expression, which on the one hand expresses the computational distance (or reference distance) an element of data is from the computing mechanism which consumes or transforms it, and on the other hand refers to the entropic cost and persistence of data and its structures, and this dual expression now requires a fundamental redefinition of “memory”.
With this, even prior to any redefinition of memory, the definition of data storage now erupts into a manifold complexity resulting from the mutually antagonistic requirements of hardware considerations balanced against software goals.
On the hardware side, there are the multi-fold constraints of physical size limitations (physically limited by heat dissipation) in storage coupled with the form factor considerations of inexpensive but slow, non-volatile sequential access disk file storage, versus the much more logistically expensive but fast, volatile random access byte storage, multi-fold physical considerations which also demand that the hardware storage of “data” be further segregated, or logistically distanced from, the hardware “central processor”.
Although the hardware aspects of storage have been mostly virtualized in present day computer systems, their constraints must be balanced against still another set of manifold considerations, found in the software costs and trade-offs of “data” representation, considerations which have now been seemingly thrown into utter confusion with this new schizophrenic definition distinguishing data as either static or temporal.
The entire drama surrounding digital computer data storage has been historically virtualized by the development of programming languages and computer operating systems, but in any digital expression demonstrating intelligent behavior, the final execution of a TSIA’s “code” can no longer afford this insulation. In the end, intelligent code can no longer afford to be distanced from the hardware conducting the pendular swing in the fundamental “clock cycle” of digital machination, because at some point, just as the data will be building the very code which will manipulate it, the TSIA’s code will be effecting incremental changes to its underlying hardware,
However, a design approach to unwind this tangled jumble of virtual (and temporal) interdependencies must resolve the issues that have sprung up from the unfortunate historical confusion between the concepts of “memory” and “storage”, a product of the academic clash between the hardware world of digital computing and the co-evolving, complex, software world of binary representation.
(At this point in the dialog, the venture of engineering true artificial intelligence will not delve into the intentional aspects of a generational evolution in TSIA hardware, driven by the virtualities of an intrinsic, engineered TSIA intelligence, as there cannot be a discussion on evolved hardware until that intrinsic intelligence is developed. This shall be a conversation which is reserved for Part Three of the Digital TSIA, so presently the dialog will focus on TSIA engineering given the current state of contemporary digital computing).
Now, before the TSIA engineer gets the impression that the conversation is moving toward the design of another specialized computer “operating system”, consider how biological intelligence came about.
In the biological brain of mammals, Nature also found the necessity to make similar compromises between the “hardware” of neural organs, and the “software” represented by the communication activity between neural elements.
Although the hyper-connected architecture of biological brains is radically different than the central-processor model of conventional digital computers, Nature still had to balance the ever-present realities of physical limitations against the necessities of functional behavior.
And while developing the functional behavior of mammals, Nature discovered, just as the TSIA engineer will discover, that there is a finite point at which local neural processes transition to global behavior, a subtle change in perspective at which there emerges a separation in the cognitive distance between apprehension and determination, an almost imperceptible shift which separates sentient creatures from all other organisms. It is at this point that Nature could evolve her “operating system” for the neural complexes which would eventually develop intelligent behavior, and it is at this point that the TSIA engineer should focus her design intention.
For those countless millennia, during which Nature was fashioning that neural enterprise which culminated in intelligence within the Homo Sapiens species, Nature encountered the same experiential situations that our TSIA must deal with, situations which present to any adaptive organism the penultimate environmental dilemma: At some level of processing, there will arise mutually contradictory conditions representing alternative possibilities.
This situational dilemma gave rise to evolutionary selection pressures to evolve a decision making faculty in some neural organizations, supported by a perceptual apparatus which could attend to distinct subsets of a particular perceptive environment, in a mutual symbiosis where the selection of those distinctive subsets of perception was concurrently modulated by the decision making faculty being informed by that perceptual apparatus. (This reference to “distinct subsets” should sound familiar here).
The evolution of this decision making faculty introduced the notion of stable states within the neural assembly, and prompted the formation of networks displaying local recurrency and positive feedback, which allowed for faster convergence and mutually reinforcing behavior, further leading to the development of global ensembles in distributed activity.
But this demonstration of global stability in the brains of organisms, brought about from the very basic building-block neural aggregates which Nature developed in the form of phasic assemblies of neurons, (assemblies needed to signal the discrete states of an organism’s environment), did not have the temporal behavior needed to signal the very changes in those states, changes which would represent the dynamics of that organisms’ environment.
For this, Nature had to evolve metabotropic behaviors into some classes of neurons, above the ionotropic functionality of neurons already developed, which could synthesize the elementary abstraction of state change in their individual signaling, which, coupled with tonic coalitions of neurons that were collectively designed to resist change within their dynamic signaling, provided a neural behavior that had the adaptive ability to survive in a dynamic, changing environment.
And certainly, it is the objective of the TSIA engineer to model this adaptive behavior. But how can the TSIA engineer make use of present-day digital computing hardware to bring about this behavior in an artificial manner?
Now, it might seem somewhat incongruous that the engineering plan for our TSIA would consider the structural implications of “data” before even addressing the “code” that might manipulate it.
But when the TSIA engineer observes that “data” is not just a static abstraction, as it has been historically characterized as by the computer science community, when the TSIA engineer understands that it is in effect, a dynamic, temporal entity having manifold properties, then that observation might lead to the conclusion that, (in its most temporal sense), all “data” should really be considered to be, “future code”.
Much like an egg can be looked at as a “future chicken”, instead of perhaps an immediate breakfast, the temporal aspects of “data” should be given greater consideration than even its immediate semantic aspects. But because of the fact that historically, digital “data” has been flaked and formed by computer scientists solely according to its immediate semantic and storage aspects, there has been almost no formalization of its temporal nature when computer operating systems and programming languages are designed.
If the TSIA engineer begins with a dichotomous understanding of “data” according to its temporal nature, and only then considers its immediate semantic characterization, this mindset will lead to a totally different perspective on data storage, and ultimately a fundamental redefinition of “memory”. The TSIA engineer must banish any and all connotations of hardware storage when defining “memory”.
According to our definitions so far, “data” must be thought of as either static, semantic symbology or as real-time dynamic signaling, but the trick in the mindset of the TSIA engineer here is that semantic symbology, although characterized as “static”, can also have a temporal nature. This temporality comes about when we realize that there is a fluid relationship between the “source of data” and the “storage of data”.
As much as there is the classic circular paradox of life, exemplified by a chicken laying an egg, which becomes another chicken, which lays another egg, there is a similar circularity within the digital realm, a circular temporality in the relationship between the source of data, and the storage of data. Just as in biological life, in synthetic intelligence the “data” is the code.
This conceptualization works if the TSIA engineer always thinks of “data” as constantly being in some form of (virtual) motion, except when being converted from one form of storage to another. Using an economics metaphor, just as the concept of a “currency” remains a static abstraction when considered solely by the quantity of currency that has been issued by a government, the “velocity of money”, the degree to which money changes hands, marks the true socio-economic definition of that currency.
The quirk in this thinking of data, which takes some getting used to, is the idea that data storage still refers to “data in motion”, but in a relative sense to all of the other forms of “data”. This may seem incongruous for the TSIA engineer initially, until one is reminded that our contemporary thinking regarding “data storage” in general is wholly outdated, and will require entirely new metaphors for the intelligent digital age.
And it is an abstraction of this concept of data in motion which forms the new, intelligent definition for “memory”, which might tease out some insights in the mind of the TSIA engineer toward the first, perhaps vague pictures of what the future, intelligent TSIA hardware might look like.
“Memory” as now defined is a property of the code which possesses it, and this property also has a dual, simultaneous nature (which by the way, as the TSIA engineer is hopefully coming to see, confirms that there is a duality in just about every definition of an intelligent nature), which shifts the connotation of “memory” more toward a focus on the temporal aspects of data, wholly removed from any static denotations of storage and encoding.
Metaphorically speaking, consider for a moment that, at the molecular level in just about every biological cell, there is a process that Nature employs that is called phosphorylation, which is a chemical operation having the property to activate some proteins and deactivate others. Phosphorylation can be readily reversed, and can serve as a digital switch, turning the biochemical activity of a protein in a cell on or off.
And at a similarly elemental level, “memory” is a virtuality which acts as the catalyzing agent in “code” to modulate the fluid nature in the circular cycle of a data source changing into data storage, which then can be “catalyzed” into another data source. And this virtuality brings the conversation to another essential definition: That of Local Storage, (our contemporary connotation of “memory”), a definition which comes about when we abstract the property of persistence (aside from permanence) and a definition which, predictably, also has a dual nature.
“Intelligent” memory refers mainly to the persistence of data (after its induction or creation – induction as static symbology or dynamic signaling, or creation as the simple product of a transformation) in dual terms of storage and function, and refers to “data” when not in motion. It reflects both the computation costs of encoding data (for storage, access or transformation) and the entropic costs of retaining data (a cost denominated by one aspect of the persistence in static symbology) after its sourcing.
Local Storage is the secondary demand to encode data transcribed from a data source in such a way as to reduce the computation distance between the data and its functional target, without the considerations of storage limitations or storage access.
These distinctions must be explicitly made in such a fundamental manner in order to be harmonious with the Logic of Infinity in any “intelligent system”, and these distinctions shall form the basis for what is termed the Ontophonic Theory for digital computing in an infinite domain. Ontophonic structuring builds that scaffolding needed to bridge the mnemonic distance between the mechanisms of, and the components representing, natural language reasoning, the four Ontophonic levels of semantic inference, logical implication and mathematical definition.
So, to satisfy that time-honored demand by academia that all scientific endeavors be quantified, the Ontophonic Theory for digital computing in an infinite domain will first put forth the definition of these complementary costs of encoding and retention, defined at the very elementary level of data abstraction, to provide that quantifiable basis for the engineering of artificial intelligence in any digital mechanization.
And also, at this point, before outlining the broader perspective needed to grasp the foundations for this Ontophonic Theory for computing, the TSIA engineer must be reminded of the true reason that the Von Neumann digital architecture is for the most part unsuited for artificial intelligence: There is a cardinal maxim in the Ontophonic Theory which asserts that any data structure that is established for data storage ultimately fragments every data structure established for time representation.
For which the astute engineer should recognize as creating another design dilemma, related to the dilemma brought about from the paradox of time, because it is the fundamental task of an engineered TSIA Executive itself, (and not the TSIA engineer), to create those very data structures that directly represent continuous time.
Back to Digital Basics
Until the mid-1960’s, computer programming was more of a craft than an engineering discipline, and the growing size of computer programs produced an exponential increase in design complexity.
The revolution that changed the craft of trial-and-error computer programming into software engineering was triggered by Edsger Dijkstra’s idea of structured programming in 1972. The idea that the GOTO statement was considered systemically harmful to program structure became an organizing principle that replaced the puzzle solving mentality of machine coding with the assertion that software of any complexity could be designed with just three basic control structures – Sequence (begin control entry/end control departure), Alternation (if-then-else), and Iteration (while-do), structures which could be nested over and over in a hierarchical structure.
The benefits of structured programming were immediate. The design of complex programs could now be abstracted and even occur concurrently with their coding implementation as the management of large projects could be modularized, and their progress and resource application measured in a top-down, direct way.
However, even with this early computer programming orthodoxy to manage the expanding complexity in computer software engineering, information systems development emerged to show a much broader perspective for digital system design than the limited considerations of software development and implementation. For instance, the operations of a business involve all kinds of data that are transmitted, stored and processed in all kinds of ways. The total data processing of a business is defined by the activities of all of its people and data appliances, as they interact with one another, and with customer, vendor and government people and appliances outside of the business. In a large company, it is a massively parallel operation with many thousands of interactions going on simultaneously.
In time, Information Systems became the predominant paradigm to automate more and more of the information processing in businesses, and for these systems, a complete description of their data operations led to a data flow jungle that was even more tangled and arcane than the control flow jungle of software development.
This interwoven complexity was highlighted by one of the original, functional problems encountered in digital program design, an issue called the mutual exclusion problem, an issue that haunts every computer programming design that does not recognize the fundamental, temporal distinctions between “storage” and “memory”, and a problem which emerges as the first critical bottleneck in the engineering of any self-adapting, temporally-aware digital software.
In computer science, mutual exclusion is a property of “concurrency control”. It is the design requirement that one thread of execution never enters its critical section during which the thread accesses a shared resource, such as a shared local random access storage cell or shared disk file.
This problem was originally solved by the implementation of hardware “shared resource” controllers to assert singular access to shared resources, but this implementation introduced other complications, variously termed as process deadlock, where a resource controller first locks out a resource to allow a particular process to access it, after which that particular process encounters an exception condition or an interrupt condition, and because of process non-completion, fails to signal a release of the shared resource, locking out the resource for all other processes.
With the academic study of concurrent computing (the form of program execution in which several computations are executed concurrently, instead of sequentially, with one process completing before the next one starts) as a property of a digital system, design methods of digital programming changed the focus from algorithmic structuring needed for problem solving, to design methods of digital process control needed for concurrent and distributed digital system behavior.
This shift in design methodology was further compounded with the advent of the Internet, where the digital landscape experienced an exponential proliferation of digital devices into just about every area of life.
With this there emerged a proliferation of different programming languages – and programming metaphors: Object Oriented design, Functional Programming, along with the Internet inspired class of languages to support scripting and device virtuality.
But none of these languages addressed those fundamental limitations of conventional digital programming design, where, in essence, digital designers commit their runtime programs to instant obsolescence whenever they create a computer program to solve a specific problem.
The real aspect that continually challenged the top-down, hierarchical design methodology in conventional computer programming, was that the entities for which software models are designed to describe, and essentially the problems they are designed to solve, change over time.
And so none of these languages fully addressed that most compelling question in software engineering: How can digital designers create a program which solves a real world problem that may not be encountered until after runtime?
To even begin to answer this question, digital designers will first have to reconcile the mutually antagonistic aspects of those three most intractable constraints of computer programming, so far remaining intractable because they have been addressed separately by differing factions of computer science and information systems research. This means that the TSIA engineer must adopt a bottom-up approach to software design, one that begins by simultaneously addressing those three constraints within a ground level, unified conceptualization of the concept of “data”.
Those early 1970’s and 1980’s digital system structures, languages and programming paradigms all formed a hierarchical state machine methodology for software engineering, and their software counterparts were called data abstractions. Their common feature is the presence of a state, represented in stored data, and accessed and altered by procedures that collectively define the state machine transition function.
Since these data are accessed and altered by reusing the data abstraction, or “object”, the hierarchy is a usage hierarchy, rather than a parts hierarchy, in a procedural paradigm sense. That is, data abstractions appear in the hierarchy at each occasion of use in the design, rather than as a part in the design. The most well-known example of this data abstraction is the “window object”, which forms the foundation for the operating systems developed by Microsoft Corporation.
This usage hierarchy of data abstractions initially showed promise to untangle the effective dual decomposition of data flows and processes in information systems, but they were concepts which did not acknowledge any of the conflicting realities in the temporality of data storage.
Data flows are convenient, heuristic starting points in formal information systems analysis, but they require a mental discontinuity to move into applied information systems design, so they encountered their own issues. The problem is that data flows describe all that can possibly happen with data, whereas processes must deal with data an instance at a time and prescribe precisely what will happen at each such instance.
Each use of a data abstraction is an instance of data flow through a process, which provides for storage in its state as well, and the collective effects in the usage of the data abstraction throughout a hierarchy is generally summarized by a data flow through the process. However, (somewhat predictably), this abstraction became a design challenge, because of the historical confusion between the constraints of hardware storage and the requirements of software representation in “data”.
Around 1987, a software concept was developed, called the Box Structure methodology, which developed the usage hierarchy of data abstractions in a way considered especially suited for information systems development.
This methodology defined three distinct forms for any data abstraction, called a Black Box, the State Machine, and the Clear Box.
A Black Box defines a data abstraction entirely in terms of external behavior, in transitions from source to responses.
A State Machine defines a data abstraction in terms of transitions from a source input and an internal state memory, with the transition establishing both a response and a new internal state.
A Clear Box defines a data abstraction in terms of a procedure that accesses the internal state and possibly calls on other Black Boxes.
The Black Box form of the design methodology gives an external view of a system or subsystem that accepts input, and for each source, produces a response (which may be NULL), before accepting the next input. The system concept of the Black Box could be a hand calculator, a personal computer, an accounts receivable system, or even a manual work procedure that accepts input from an environment and produces responses one-by-one. As the name implies, a Black Box description of a system omits all details of internal structure and operations and deals solely with the behavior that is visible to its interface in terms of stimuli and responses. Any Black Box response is uniquely determined by its stimulus history.
The idea of describing a system module as a Black Box is useful for analyzing the system as a whole from the point of view of the module interface. Only system externals are visible, and no module procedures are described.
The State Machine gives an intermediate system view that defines an internal system state, namely an abstraction of the data stored from input to input. It can be established mathematically that every system described by a Black Box has a State Machine description, and the State Machine behavior can be described by the transition formula:
(Stimulus, Old State) —> (Response, New State)
Much of the work in formal specification methods for software applies directly to a specification of the State Machine view. These methods specify the required properties of programs and abstract data types in axiomatic and algebraic models. The models represent behavior without presenting implementation details.
The Clear Box definition, as the name suggests, opens up the State Machine description of a system module one more step in an internal view that describes the system processing of the stimulus and state, in which that box’s behavior is described in terms of three possible logic structures, namely sequence, alternation and iteration, and a concurrent structure.
The methodological aspect of this arrangement is the representation of every logical step (be it a data reference, logic switch, or iteration) in the processing of a module. It is also enclosed by the abstraction of a new state transition symbol as defined by the transition formula.
The relationships among the Black Box, the State Machine and the Clear Box views of a system module or subsystem precisely define the tasks of information derivation and expansion.
It is a derivation task to deduce a Black Box from a State Machine, or to deduce a State Machine from a Clear Box, whereas it is an expansion task to induce a State Machine from a Block Box or to induce a Clear Box from a State Machine.
That is, a Black Box derivation from a State Machine produces a state-free description, and a State Machine derivation from a Clear Box produces a procedure-free description.
Conversely, a State Machine expansion of a Black Box produces a state-defined description, and a Clear Box expansion of a State Machine produces a procedure-defined description.
The expansion step does not produce a unique product because there are many State Machines that behave like a given Black Box, and many Clear Boxes that behave like a given State Machine.
The derivation step does produce a unique product because there is only one Black Box that behaves like a given State Machine, and only one State Machine that behaves like a given Clear Box.
Now, although the Box Structure design paradigm still suffered from an inversion of program design, (every Black Box regressively assumes the existence of some program structure around it), which ultimately resulted in its disuse, the concept did formalize a distinct separation of the hardware aspects of state definitions, from the data abstractions of the model as a whole.
This early work in academic computer science and information systems gave way to artificial intelligence research which looked for simple and powerful reasoning techniques that could be applied to many different problems. A classic example is the work of Newell, Shaw and Simon on a computer program called GPS. Intended to be a general problem solver, GPS could prove theorems and solve puzzles and a wide variety of logical problems.
Unfortunately, attempts to apply such general methods to larger and messier real-world problems were mostly unsuccessful. In their early methodology, they approached problem solving by attempting to reshape a problem into a form their programs could work on, as opposed to the process of reshaping their programs into a form that reflected the problem. Nor could these general methods, by themselves, cope with the enormous search spaces of alternatives, which were created by that inverted design approach to begin with.
How do people cope with these same problems? People rarely solve problems by reasoning everything out from first principles. People create heuristics.
Recognizing that heuristic knowledge is as important as reasoning and inference, this early AI research worked on a variety of methods for representing and using knowledge. Although a very necessary component, the discipline of structuring intellectual knowledge for problem solving failed to address the more compelling requirement to induce new knowledge in the first place, (so-called experiential knowledge, a process which Nature developed hundreds of millions of years ago, which is essentially a fundamental process of resolving the sub-dimensionality in apparent non-linearities, a process the AI community began attempting to model, but have since been distracted from, with their misplaced focus on the modeling of “learning”).
Early AI research also grappled with fuzzier kinds of problems, where logic is supplemented by heuristics based on human experience and judgement. One result of that research was the development of so-called knowledge-based expert systems – programs that exploit a collected base of focused knowledge to solve problems in specialized areas.
But these systems still did not resolve the fundamental requirement to produce new knowledge also, relying on human processes to initially build the knowledge base itself.
These expert systems did, however, begin to establish critical boundaries in the enterprise of mechanized intelligence, definitive abstractions that could form the needed delineations to general problem solving, beginning with this first critical boundary:
Internal Representations <—> External Forms
Internal representations should reflect external forms, not the vagaries of hardware storage or software definitions.
One of the first computer programs to pierce the limitation in the lack of knowledge generation was actually one of the first of the knowledge based systems, as demonstrated by the Dendral system, begun in 1965 by Feigenbaum, Lederberg and colleagues at Stanford University.
Many problems in graph theory, game theory and other areas of discrete mathematics can be posed as search problems. These problems are characterized by the existence (at least in principle) of a systematic method for generating candidate solutions, as well as a systematic method for testing acceptability.
However, in the case of genuinely interesting problems, the number of candidate solutions is usually so great that an exhaustive search is infeasible. Therefore, any device that significantly reduces the amount of search required (preferably without compromising the quality of the solution) is called a heuristic, and a search strategy guided by heuristics is called heuristic search.
The Dendral system was concerned with using knowledge to limit search, by generating plausible structural representations of organic molecules from mass-spectrogram data, nuclear-magnetic resonance data, and additional constraints provided by the user.
And although further establishing those critical boundaries, like all of the knowledge-based productions researched by academia, even the promising areas of heuristics, Dendral failed to address the mechanisms that could expand the sphere of knowledge outside of a closed search space. The sphere of Infinity.
As the paradigm of expert systems was expanded in subsequent works, research in a more enterprising computing approach became widespread with the first International Conference on Artificial Neural Networks in 1987.
This paradigm was widely embraced by the AI community, as the academic allure of a mechanism which could generalize the geometric boundaries within a given symbolic data set was realized.
The principle of artificial neural networks has always been considered to be the next step in explicitly representing human knowledge in general, by demonstrating how to transform denotative knowledge into models of applied knowledge.
These connectionist approaches to computation initially began with a bottom-up, biologically inspired approach to representation, where concepts are identified using individual nodes, with relationships among them encoded by excitatory and inhibitory links, and where the computation proceeded by spreading activation and lateral inhibition.
But these connectionist approaches became obtuse in their applicability, because the architecture attempted to generalize already abstracted symbolic data, using elements that replaced the temporal behavior of spreading activation with a static abstract state (called “weights”), and the design paradigm also defined elements that were stripped of any inhibitory behavior, which prevented the network from displaying any lateral inhibition.
Nor did the deceptively simplified models of artificial “neurons” capture the true mechanisms that “learn”, the true learning mechanisms which Nature engineered into her biological neurons. (Within the dendrites of pyramidal neurons – the most abundant of neurons in the mammalian cerebral cortex – there are dual ionotropic receptors, termed AMPA and NMDA receptors, labelled after the forms of neurotransmission they are receptive to, and it is the diversity between the behaviors of these complementary receptors that is what forms the active channel for “learning” at the biological cellular level, expressed as the neurological modulators to the behavior of spreading activation in coalitions of neurons, behaviors which are wholly absent in the overly simplified artificial neural network model).
In an effort to expand this constricted applicability of neural networks, there were incremental developments in the distributed encoding methods for representations, such as recurrent networks designed to save hidden unit activations in separate layers for feedback to the input layers (in an attempt to encode temporal symbolic knowledge as finite state automata), and convolutional networks with pooling layers for complex classification and regression tasks, but since these models did not fundamentally alter the gradient-descent algorithm of the network, they could not provide any semantic boundaries for structured representations, due to the general difficulty that feedforward networks have for representing nonlinear relationships in data sets.
Additionally, the limitations of artificial neural networks have led to another research dilemma. Once an artificial neural network has “learned” a generalization, it is unclear how to extract the implicit representation of that knowledge. After the generalization is internalized, it cannot be transplanted to an external computing mechanism.
But at least the conversation on the methods of symbolic artificial intelligence was becoming more focused, more toward the process of automated model creation itself, rather than the broader goal of building general purpose problem solvers. And in this conversation, the representation and manipulation of symbolically structured knowledge plays a central role. Indeed, it was the goal of expert systems to explicate the “knowledge” from reasoning in a problem domain that led to their wide allure.
However, since general, unconstrained artificial neural network architectures are not necessarily able to facilitate the representation of symbolic knowledge within the network, the architecture cannot allow a direct correspondence between external symbolic knowledge representations and internal “learned” generalizations. Artificial neural networks have a “black box” nature in their learning, which is certainly the reason for their wide academic acceptance.
And so, in order to pursue the implementation of a true, artificially intelligent mechanism, this internalization behavior in the artificial neural network architecture must be changed to reflect a “white box” nature, which would allow the internalized generalizations of an artificial neural network to be externalized. Even with the development of the ANN methodology, there still remains the goal of intelligent systems to exploit the synergy between symbolic and neural processes.
In theory, an artificial neural network has the ability to encode complex decision regions by linear and nonlinear transformations of its inputs. Its “knowledge” about this encoding is found in the numeric values of the so-called weights of the network, which make neural networks good universal approximators, and with a proper fit of architecture, they are good classifiers and resistant to the presence of noise. But this is offset by numerous drawbacks. The first of which is the necessity for the prior specification of a network organization. If the size of the network is too large, it generalizes poorly, and if it is too small, learning becomes insufficient. Setting the size of a network itself presents a scaling problem, as the computational cost grows rapidly as the network size increases.
And equally problematic, the data sets used to build a machine learning systematic can be noisy, conflicting and sparse. And the extent to which prior knowledge is used to preprocess data sets, to configure the network model of connections, topology and weights, and to train the network, this preconditioning serves to bias the resultant behavior of a network, and consequently blurs the boundary between external knowledge representations and internal generalization structures.
In their early form, connectionist approaches to “machine learning” implied a metaphor that expressed a trade-off in learning which reflected that the less knowledge of a problem you have, the more data you need for learning. Conversely, the less data you have for learning, the more prior knowledge you need. In more general terms, learning can be viewed as the task of bringing a-priori knowledge to bear on the available data in view of extracting a-posteriori behavior from this data. (Certainly, here, the perceptive TSIA engineer should recognize the same inversion of design which doomed the Box Structure information systems methodology previously mentioned, where the computing mechanism always regressively assumes the existence of some program structure around it. Keeping this recognition in mind will be essential to understanding the broader complexions which do lead to a successful AI design.)
There is a wide range of possibilities between pure knowledge-driven and pure data-driven learning. The problem of combining knowledge and data can be addressed from multiple angles. At one end of the spectrum, one can use data to improve knowledge-driven learning, and, alternatively, one can use prior knowledge to guide and reduce search during data-driven learning.
But neither of these metaphors addresses the neurosymbolic integration of symbolic representations within neural network topologies. Controlling the knowledge-data trade-off in machine learning goes beyond the simple mapping of symbolic structures into neural networks.
In pure neural network learning, there is a dilemma between what is termed bias and variance. Bias captures the notion of systematic error for all training sets of a given size, it is that part of the error that depends only on the learning model or architecture of the network, or more precisely, the number of free parameters. Its contribution to the error can be diminished only by adjusting model complexity.
Variance, on the other hand, depends on the training sample. A model that is too complex or too flexible in relation to the training data leads to large variance.
The trade-off between bias and variance is such that reducing bias often increases variance, and vice-versa. To reduce bias, developers add structure to the model, perhaps by adding hidden units, but increasing model complexity may lead to higher variance. Finding a compromise between the conflicting requirements of bias and variance in order to minimize the total generalization error of a model, pushes network design into the realm of art and craft, and away from design engineering.
Although the role of prior knowledge in mitigating the bias-variance dilemma seems evident, introducing symbolic representations into a pure neural network creates its own particular dynamics in the bias-variance dilemma.
At the other extreme, where domain knowledge is scarce or unusable, neural network design techniques rely mainly on guided search. These knowledge-free methods can be subdivided into dynamic and static methods. In a static configuration, the network topology is chosen before the training process, whereas in a dynamic configuration it is dynamically modified during training.
Another research challenge consists of widening the range of knowledge types that can be incorporated into neural networks, as well as the repertoire of techniques for incorporating them. This implies tackling a number of representational issues, the foremost of which is the restricted representational power of state-of-the-art neural networks.
It has been accepted for some time that artificial neural networks cannot be expected to learn anything useful without any prior structure. The computational capabilities of feedforward networks are sufficient for learning input-output mappings between fixed, spatial patterns that are invariant over time, but these architectures cannot generalize time-varying spatial patterns. The class of recurrent neural networks that has been developed to model time-varying systems still suffers from issues of temporal knowledge representation, due to their inability to model structured representations.
Structured representations are ubiquitous in different fields such as knowledge representation, language modeling, and for sure, general problem solving. While algorithms that manipulate symbolic information are capable of dealing with highly structured data, adaptive neural networks are based on strong modeling assumptions and are usually regarded as generalizing models for domains in which instances are organized into static data structures.
This inability of ANN’s to generalize structured representation was highlighted by the so-called “Two Spirals problem”, which was proposed as a task constructed to test the ability of neural networks to deal with complex decision regions. This well-known benchmark differed from many others by testing only the memorization ability of the ANN model, rather than its ability to generalize over the problem domain, and brought out the crucial inability of ANN architectures to dimensionalize their generalizations.
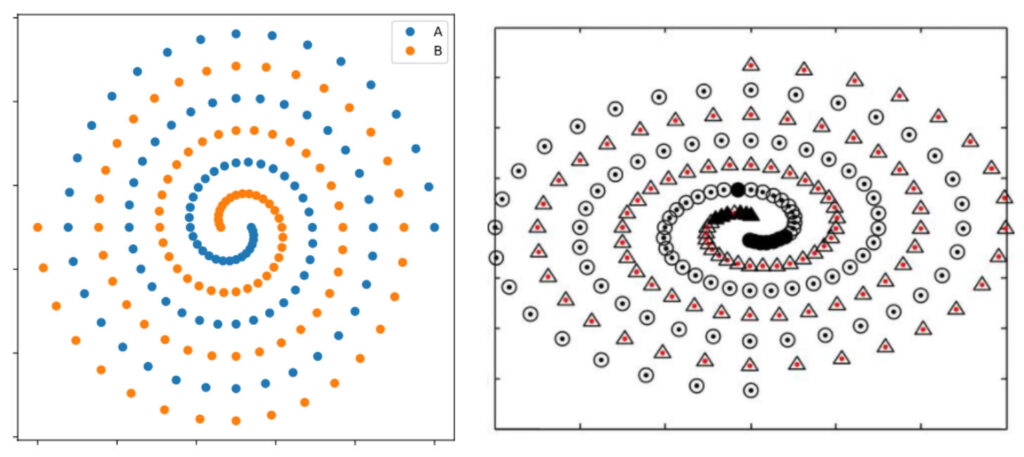
In its zeal to efficiently conduct the gradient-descent algorithm, the artificial neural network model attempts to generalize the geometric distribution of the twin spirals in the Two Spirals problem solely from an entirely spatial perspective. But because there is a decision step, requiring the temporal decision of a local distance between prior local classifications, (which must be remembered before the next spatial distance classification can be made), the model cannot perform the global distinctions necessary to “comprehend” the complementary geometry.
Artificial neural networks are incapable of any gestalt understanding in any of their representations.
And this limitation is manifest even before we acknowledge the inability of the ANN model to discriminate true cyclic events, or to generalize pure impulse (nonlinear reversal) events. Although many processes that constitute the mind can be understood through the framework or neural networks, (biological or artificial), there are others that require a more holistic basis.
So we find that this limitation draws the discussion away from the constrained, neural network perspective of “learning”, and returns the conversation on the engineering of artificial intelligence in general to the more expansive subject of self-adaptive, temporally-aware systems, and specifically to the mechanization of systems which can create models of dynamic systems themselves, as opposed to the myopic view of AI which has been embraced community-wide to model “machine learning”.
Artificial intelligence research is more than just learning and modeling a specific data set, it is a methodology of engineering a mechanism which can develop its own models of dynamical systems.
But the TSIA engineer cannot make the mistake of approaching this conversation with the typical hierarchical approach favored by academia, so the engineer must assume a bottom-up mindset of intentional design, a mindset which acknowledges that the key to engineering self-adaptive mechanisms must start at the most elementary level of those mechanisms, by distinguishing between the fundamental temporal semantics which separate events from processes. And we find that there is an even more elemental design consideration here, which is the need for a common atomic concept to unify these separate semantics at the same level of their division: That atomic concept is the representation of continuous time in a mechanism composed of discrete elements.
In 1910, Albert Einstein encountered the nuances of this elemental mindset when he set about to describe the grandest of dynamical systems: the Universe itself. At the time, he realized from the onset that the very essence of any description of the Universe must start at this most fundamental level, at the level of the enigmatic fusion of Time and Space, which is our experience of the dynamic world, and which forms the very definition of our “consciousness”.
In order to formulate his models, Einstein recognized that his mathematics must first and foremost reflect the co-existence of time and space in any representation of the physical world, rejecting a top-down separation of concepts over a bottom-up fusion of concepts, and so he adopted a branch of tensor calculus as the representational structure for his derivations, and subsequently as the mathematical basis for the formalization of his famous equations.
However, even if a systems modeler does begin with this bottom-up, inclusive approach, the success of implementing an approach which defines a dynamical system solely within a mathematical framework is possible only when the system being modeled is a closed system. A purely mathematical framework was possible for Einstein because modeling the Universe itself is the ultimate “closed system”. There is nothing more open than the closed system of the entire universe.
In contrast, the previously discussed “Box Structure” metaphor in information systems development began as a very powerful paradigm, but it ultimately and unfortunately broke down in subsequent application because it could not open up to a space of infinite states.
Many engineering problems share some characteristics of both system definition and parameter estimation in the modeling process. As the dominate technique for modeling dynamic systems, differential equations are very useful tools, because the causal relations between physical variables present in engineering problems can be described well by differential expressions.
And even in dynamically interacting systems, where closed loop behavior, both feedforward and feedback, is defined within a mathematical framework, differential equations can establish boundaries between temporal and spatial generalizations, but where the model also requires the parametrization of some dynamic in the generalizations themselves, as in the Two Spirals problem, most purely mathematical modeling approaches break down.
Additionally, models which implement purely mathematical or logical structures to describe of open-systems, where some of the dynamics of the system might be unknown, cannot even get off the ground, because the axiomatics of symbolic mathematics, (and equally the true-false semantics of Boolean logic) have no definition for the “unknown state”.
So even before developing any definitions for this “unknown state”, to be sure, even before the TSIA engineer can devise expressions for any state whatsoever, the prior basis for that expression must establish the very ontological identity which emerges between Time and Existence, an expression which is established not within a deep, intellectual discussion, as is the habit of academia, but within a formalism that can be mechanized.
Nature accomplished this mechanization when she evolved the formalism of metabotropic processes in certain mammalian neurons. But since the behavior of mammalian neurons is beyond any economic modeling in a digital framework, the TSIA engineer must devise a synthetic mechanization of this behavior, one which still provides for the expression of infinite states within an emerging ontological identity, an inseparable duality which asserts that Time is Existence, and Existence is Time: The Paradox of Time.
In the realm of radio communications, in order to receive a radio transmission, every radio receiver must have a stable timebase that allows for the accurate reproduction (in the receiver) of the frequency wave on which the “information” in a radio transmission has been superimposed (at the transmitter). Being able to reproduce the “carrier wave” of a transmission allows the receiver to “subtract” the reproduced wave from the received signal, leaving just the “information” that was superimposed on the carrier, which is essentially the basic idea of radio transmission
But in the realm of neural processing, there is a shift in the relationship between “time” and “information”, a relationship that gets lost when neuroscientists attempt to use the metaphor of radio communications (or the concept of “information transmission”) when describing neural behavior.
In the world of neural processing, neural networks cannot reproduce the “carrier signal” on which any “information” has been superimposed. And it is even more difficult to bring the entire metaphor of ‘signal modulation’ into the realm of neural processing, but that is just what AI researchers attempt to do when they speak of the “information” present in the neural behavior of sensing an environment.
So the TSIA engineer must understand how the analogy of superimposing “information” onto a “carrier signal” immediately limits and restricts our ability to understand the true behavior that neurons exhibit when they “process” the sensations arising from their environment.
And this shift in relationship also applies when we see the different relationship that “time” has to “information” in the realm of symbolic logic compared to the realm of neural processing, especially if the TSIA engineer were to substitute the concept of “existence” for the concept of “information” when making the comparison of symbolic logic to neural processing. (Recall how binomial logics necessarily conflate predications for existence with their predicates for relations).
However, there are aspects to this metaphor of signal modulation which have been useful, which is why it has endured throughout the many decades of neuroscientific research, aspects which the TSIA can retain, if it is kept in mind that the overall metaphor of ‘signal modulation’ is conceptually distracting. This means that the TSIA engineer should begin the conversation having only a fuzzy understanding in the relationships between these domains of “time”, “signal” and “information”. Since we cannot define any behaviors within whole assemblies of neurons before we define the behaviors of individual neurons, we must also understand how the relationship between these three domains shift as we move from describing the behavior that individual neurons demonstrate, to describing the behavior of assemblies of neurons.
The nature and character of “signaling”
Within the conceptual realm of the TSIA, there have been a large number of references to signaling, used in many contexts.
To provide a more precise definition to the term, it is important to first specify a number of its varied connotations, and make a number of important distinctions.
The semantics of “signaling” and “information”, when used in the context of neuroscience, began to get confused when the several different connotations of the root term “signal” were applied equally to biological neural behavior.
The term “signal” has two distinctive connotations, depending on whether it is applied to semiotics, or to communications.
In the study of semiotics, a “signal” may be considered simply as an interruption in a field of constant energy transfer. However, when used in the discipline of communications, the term “signal” carries a slightly different connotation, where it is considered to be an interruption in a field of constant energy transfer which has a common interpretation between sender and receiver. (It is this connotation that we very much want to avoid).
So this dialog will be specific in its connotation of “signals”, and specify the interpretation of “signals” to be simply an interruption in a field of constant energy transfer, and “signaling” to connote the sensical apprehension of “signals” as thus defined.
But this specificity regarding the connotations of “signals” still leaves us with a lot of room when interpreting it in the context of “signaling” within the confines of a biological neural array or TSIA.
So, beginning with an initial perspective focusing on the TSIA/environment interface as a reference, our engineering plan will consider the “signaling” that results from an entropic signal in the TSIA’s environment (that is transduced across the TSIA/environment interface) to be termed ‘modal signaling’ (and we will begin the characterization of all entropic signaling that originates outside of the TSIA as some form of ‘extero-signaling’).
Now, we want to enlarge that perspective somewhat, because the entire concept of “signaling” within the TSIA will be pictured as essentially one great circle, representing the progression of internal signaling as it diffuses through (and simultaneously shapes and remodels the varied processes of) the TSIA, which comes back around to be released back into the environment as some agency or direct participation of the TSIA in its environment.
And acknowledging that the TSIA is not a static entity, and the environment is ever-changing, we have not a unitary circle, but in essence the dynamic rotation of a great many rotations (what we shall envision as the TSIA temporo-signal helix, which conceptually is a continuous rotation of the cyclic processes as a TSIA “grows” through the comprehension and adaptation to its environment). This helix represents the fact that our TSIA is never the same as it was before a specific instance of modal signaling traverses the circularity of internal “processing”.
The acknowledgement of this means that, not only do we have to be specific about the modal signaling that is a functional product of the extero-signaling , the characterization of all internal signaling itself morphs as modal signaling diffuses in its traversal through this circle of modal signaling, changing to TSIA manipulations of its environment, and we must specify the various forms in that change and differentiation.
But before we settle in and expand upon our definitions of signaling internal to the TSIA, we should visualize some essential relationships in extero-signaling that will be occurring outside of the TSIA. And in order to visualize these relationships, we envision what will be defined as three “circles of signaling”, or, in effect, three dynamic helixes which we represent as the three circles of signaling:
Even though the perceived environment is ever-changing, that change has manifold dimensions which must also be characterized, so, backing things up a bit from the definition of extero-signaling, having characterized part of the adaptation process of a TSIA as the intentional manipulation of some direct aspects of its environment, (which we will define as ‘intentional extero-signaling’), we can differentiate extero-signaling (prior to its transduction by a modality) as ‘first-order extero-signaling’, which is that signaling which would have occurred in an environment (at a specific point in semantic time) had the TSIA not been present in the particular setting that it is inhabiting, and we can further characterize ‘second-order extero-signaling’ as that extero-signaling that occurs as a direct or indirect result of the TSIA’s presence in a particular environment.
We can consider the traversal of intentional extero-signaling, (as it leaves the TSIA to diffuse into the vast infinity of the environment), to form the initial arc of the right circle, which is tangential to the center circle of internal TSIA signaling. And we can consider the remaining arc of that right circle to be that extero-signaling of the environment as a whole which comes back around to cross the TSIA/environment interface, to appear through transduction as first- and second-order extero-signaling. And again, because this circularity is ever-changing, we must envision this second circle as actually the temporal progression of a helix much like the central circle of internal TSIA signaling.
And there is another wrinkle to all of this external signal characterization, because there is the other, third ‘circle of signaling’ which is also tangential to the circle of internal TSIA signaling, but is visualized on the side opposite of the circle of extero-signaling.
Although this next circle also represents an interface to the environment of the TSIA, the signaling that comprises it must be separated from the signaling presented to the TSIA by the infinitely changing environment, because in the course of its adaptations to the dynamic, temporal helix of environmental extero-signaling, the TSIA will be exchanging speech entropy with other intelligent agents (whether biological or synthetic).
Now, within this third circle of signaling, this speech entropy will be differentiated into ‘speech signaling’ (and although speech signaling crosses the interface from an internality of the TSIA into the exteroceptive environment, speech entropy itself should not be classed as a component of extero-signaling because there will be many “reflections” of speech entropy that is “reflected back” into the TSIA and does not cross the interface into the environment), and ‘language signaling’, which is characterized by a symbolic exchange of speech and language originating with other TSIA’s, forming a continuous arc in this other third circle. Although it occurs in a loop diffusing a TSIA’s speech and that of other TSIA’s speech, Language signaling is considered distinct from speech signaling by having the additional property of common understanding between the internal TSIA and the external TSIA, the one time that we will attach a communication connotation to signaling.
Which brings us to the wide spectrum of “signaling” that can be characterized as occurring in the center circle between environmental extero-signaling and environmental speech and language signaling, that wide spectrum of “signaling” internal to the TSIA (and most mammalian species) which has been so misunderstood and so mischaracterized throughout the history of AI research.
And the chief cause of this misunderstanding, throughout the collective AI community, and throughout the history of AI research, has been an intellectual conflation between the interrelated concepts of “signaling” and “information”.
This marks a grave error on the part of the TSIA engineer who does not, from the very beginning, understand the distinction between these two concepts, a historic mischaracterization unfortunately begun with Donald Hebb’s erroneous theory of neuron interaction in 1949, and which has since been propagated and reinforced in the decades following, due to a devout use of digital computer terminology to explain perceived biological neural behavior.
And yet, the real tragedy in Donald Hebb’s legacy was not so much his theory itself, it was in his charismatic way of describing his theory to those varied individuals of his time who did not have a neuroscientific background. Although (unknowingly) erroneous, he turned the very complex behavior of neural interaction into a catchy cliché, which stuck in the minds of many of the students and fellow researchers who followed him, a bumper-sticker conceptualization that has unfortunately hobbled neuroscientific research for decades.
However, rarely can the magnificent neural creations of Nature be reduced to a mere cliché. Especially the mammalian central nervous system, arguably one of the most complex creations in all of Nature.
And as we expand and clarify our understanding of the complex processes occurring in this most complex creation, one concept stands out: There is no hierarchical design intent behind the organization of mammalian central nervous systems which can be reduced to a bumper-sticker cliché: From any perspective they appear to be, and must be characterized as, a massively asynchronous collection of individual neurons, interconnected in a predictable phylogenetic and ontogenetic manner, individual neurons behaving in a predictable manner to the asynchronous temporal exchange of signals between them.
This is wholly unlike a digital computer, whose individual elements are, and in fact must be, organized in a hierarchical manner stemming from a central design intent, one that predetermines the interconnections between them, in a fashion that dictates not so much an exchange of signals between them, but a change in states, that is wholly devoid of any temporality.
This is the reason why the TSIA engineer must first reject the Hebbian doctrine as a theory for neural behavior, (because the doctrine doesn’t really describe the temporal behaviors of individual neurons themselves, it only attempts to describe the mechanism which promotes the interconnections between them), and second, why the TSIA engineer must also wholly abandon the use of all digital computer conceptualizations and metaphors when envisioning the actual organizational pattern of interconnections between biological neurons and synthetic signaling elements.
In the hardware design of digital computer systems, there is a fundamental distinction between those elements in a system that compute the current state of signaling occurring within the whole of the digital system, from those interconnected elements that store a computed state within the whole of the system.
Because of this distinction, all digital computer systems (whether a super computer, massive mainframe, laptop computer, hand-held iPhone, or even the embedded processors ubiquitous in vehicles and appliances) separate the temporality of computations from the context of computations. (Note that the temporality and context of signals is abstracted before the system is designed).
Without a doubt, this is a design paradigm which the TSIA engineer must be ever vigilant to avoid.
We can try to clarify this rather fuzzy concept by envisioning this paradigm as it occurs in the simplest of digital computing devices – the electronic calculator.
Here, we can envision the “signaling” occurring within the whole of the system (the current state of the calculator) as comprising all of the keys pressed in between activations of the “Clear” key (some calculators have ‘clear entry’ and ‘clear memory’ keys, but they are not relevant for purposes of this discussion).
Following this, we would envision the computation of that current stateof the system as occurring at the time that the “Equals= “ key is pressed.
And, in the simple functionality of the electronic calculator, the storage of that computation would be envisioned as the display of the numerical results.
Now, what differs between the functionality of our ubiquitous electronic calculator and every digital computer, is that in the hardware design of digital computers, the stored state of every current calculation is fed back into the process of computing a new, temporally subsequent state, which is stored and then subsequently fed back in, in a never-ending cycle of compute & store (never ending as long as the power switch remains on, of course).
For sure, the TSIA engineer should see that there is absolutely no functional difference in the “computation” being performed in a typical electronic calculator and the “computation” being performed in even the largest and most complex supercomputer or mainframe. The only difference between the two designs is in the size and complexity of the storage mechanisms incorporated for the sequential state products computed in either design.
And, just as importantly, the TSIA engineer should see that at no time do the computation elements themselves change in the course of the compute-store-feedback cycle. The only thing that changes, even as the “data” fed into the machine from its “environment” changes, is the state of individual elements in the machines’ data storage mechanism.
And this paradigm (of separating temporality from context), spills over into the fundamentals of digital computer software programming as well. When we get down to the real nitty-gritty of digital computer software design, one of the most basic limits on computer program performance is not the maximum clock speed of the processor, but what is called “branch prediction”.
Branch prediction involves one of the lowest levels of theoretical uncertainty in digital computer program execution, where there is a trade-off between the predictability in the path of program branches, and the predictability in the locality of data.
Where the fetch of a word from dynamic random-access storage might be dozens or even hundreds of clock cycles away from its load command, and a fetch of local (on chip) cache storage is only a few clock cycles away, minimizing program execution time involves maximizing the number of times the processor fetches data from its local cache, instead of from dynamic random-access storage.
But placing the needed data into a processors’ on-chip local cache from dynamic random-access storage is complicated by the uncertainty of branch instructions which have yet to be executed. (Recall the programming revolution previously mentioned, that was based on the three basic control structures of Sequence, Alternation and Iteration, where two of the structures, the “if-then-else” of Alternation and “while-do” structures of Iteration, both inherently held variable branch instructions).
And when we look at the macro and global effects of data storage protocols, the picture gets even murkier, but the message is still the same: It is always the architecture of a particular data storage scheme that drives the hardware complexity of every digital computer system and its subsequent software programming approach.
Although it may not be readily apparent, the immediate solution to branch uncertainty is to store all data “close” to the branch code which switches its visibility, because, in the contemporary approach to digital computing, the locality of data becomes an abstract substitute for the temporality of computation.
Data access (even prior to any manipulation of data) involves the movement from the on-chip local cache to dynamic random-access storage, to non-volatile disk storage, then to the near-infinite boundaries of the Internet and back again, but at each stage, its location becomes just as important as its context, since, in the design, physical locality has become the abstract substitute for the temporal uncertainty of branch code.
And there is an even more insidious abstraction occurring here, one which is often overlooked but is fundamentally significant. Every movement of data from any of these hardware storage locations to another, produces a change in the binary structure of the data, a modification that also occurs apart from any computation.
Certainly, after having read the prior discussion in this dialog detailing the implementation of a tertiary logic (as the remedy for the inadequacy of binomial inference logics in dealing with the uncertainty of unknown semantics), the TSIA engineer might see how mitigating the uncertainty of binomial branch code can come about from increasing the dimensional behavior of binomial switching devices, but there are more fundamental aspects to implementing state devices in computation that must be addressed before we can begin that conversation.
However, in any case, the successful implementation of any paradigm to mitigate the uncertainty of branch code will require a revolutionary change in every aspect of digital hardware architecture and design. A revolutionary change that also must take into consideration the constraint of latency present in the Von Neumann digital architecture.
For sure, contemporary AI researchers are looking to the promise of parallel processing, (implementing graphics processing units in numbers), but again, these architectures, (including all of the “neural network deep learning” models currently favored), still suffer from the bane of all digital devices: Computing architectures that implement state devices as their basic elements must implement some data storage scheme which distances the data from the elements performing the computing on that data.
Contemporary computer programming only bridges the virtual distance that lies between an element of data and the digital computing hardware that consumes it, so we should understand that intelligent digital programming must reflect a design which reduces the virtual distance of data from its computing hardware.
So, to get to any revolutionary change in the implementation of digital architectures for artificial intelligence, we must fundamentally alter this design addiction to the use of separate storage elements for state products in the basic process of transforming “information”, and to do this, the TSIA engineer must understand the very fundamental concept that Nature herself learned hundreds of millions of years ago.
That fundamental concept, which we can call the “First step toward intelligence”, is the concept of Elementary Abstraction, which Nature learned is the fundamental movement from “signaling” to “state” in the activations of neural coalitions.
And at this point the TSIA engineer must at once see the impossibility of using state devices as elementary computing devices for artificially intelligent designs, a design intent that puts the cart before the horse as we try to implement that crucial lesson Nature learned those many eons ago: Intelligence is a process that begins with elementary abstraction (the basic movement from “signaling” to “state”), so how can we implement this abstraction with basic computing elements that by design are state devices to begin with?
In the chapter titled “Intelligent Logic Inferencing Systems”, the dialog showed the distinction between the basic elements comprising digital computer systems (including the basic elements implementing “artificial neural network deep learning” systems), versus the basic elements comprising biological neural complexes.
All non-biological “computing” elements were characterized as state devices by virtue of the fact that the “computation” occurring in state devices is “pre-abstracted”, in other words, the temporality in computations has already been abstracted away from the context of any computation, in the prior design of the computing element itself.
But this is not the case with biological “computing” elements. Because biological neurons implement an internal energy cycle of their own, Nature found out hundreds of millions of years ago that in order for her biological neurons to perform this elementary abstraction themselves, the temporality of computation cannot be separated from the context of their computation.
Global behaviors in mammalian central nervous systems come about from the gestalt progressions when moving from egocentric apprehension to allocentric apprehension, then to semacentric apprehension, and ultimately, in Man, to the crucial “sandbox apprehension” level of cognitive self-awareness of the individual in its environment.
However, all of these progressions are founded on the fundamental behavior of elementary abstraction, expressed at the neural level.
This means that our revolution in artificial intelligence computing must start with the “basic computing elements” themselves, even before we begin to envision the “plan” for their interconnection. (Or, the plan for their interaction, because hopefully the TSIA engineer is coming to see that developing global behaviors in intelligent assemblies of asynchronous signaling devices means more than the physical interface between devices, it involves the temporal interactions within that interface). And to do that, we must again revisit the history of today’s AI computing systems.
Just a little more history
Because Donald Hebb was so narrowly focused on the mechanisms that determined the interconnections between biological neurons, he totally missed the true story in the magnificent behavior that Nature crafted for neurons individually.
The concept that Donald Hebb missed in 1949, in his interpretation of synaptic behavior, was in the form of the “information” conveyed by the activation of neurons. Because he mistakenly assumed that the axonic impulse of neurons was the “information” conveyed in neural behavior, his Hebbian doctrine set back AI research for decades. Because he totally missed the concept that the “information” conveyed in neural behavior was actually contained in the measured interval between impulse activations, and not in the isotropic “spikes”, or axonic activations themselves, his Hebbian model of neurons, which tragically mesmerized a generation of AI researchers, could never truly replicate the behavior of biological neurons when scaled up to any size that could be considered “useful”.
But even if we were to look past this mischaracterization, it is evident that Hebb still fatally adapted the meme that some “information” had to be present in those neural activations to begin with.
A perspective which the TSIA engineer must mightily reject from the very beginning. However, that leaves us sitting in a very uncomfortable intellectual posture regarding the nature of the neural activations we are trying to characterize. If we say that there is no “information” contained in the activations of individual neurons, what is the phenomenon we are observing when we observe one neuron displaying a set of activations different from the set of activations displayed by another?
We will begin by saying that this “phenomenon”, what we shall simply characterize as “signaling”, is at its most basic interpretation, a “report” with no context.
Specifically, we shall say that all products of any individual “computing” element within a TSIA, shall be characterized as “signaling” no matter what the source or context of the efferents to those elements might be.
Now, this definition still leaves us with something of a contradiction. But we can begin to resolve this contradiction if we first understand that no single computing element can convey “context”, or “information”. Individual elements within a TSIA can only convey signaling.
So we must look at “signaling” more from a temporal perspective than from a contextual perspective, which is (most understandably) difficult to do at first.
But once the TSIA engineer gets past this inflection of perspective, the entire vista of intelligent computing will open up.
Certainly, perhaps it might help if the dialog were to provide a more concise definition of “context” or “information”, (and the neural elements which engage in their commerce), but the TSIA engineer must patiently understand that, by this new definition, we cannot even speak of “context” or “information” until we observe the behavior in coalitions of individual elements, and any definition of an “element coalition” is presently unobtainable until the temporal behavior of individual elements is wholly understood.
And unfortunately, we cannot divine any interpretation of “context” or “information” based solely upon the interconnection of individual elements either, which has been the conundrum that has stymied AI researchers for many decades. Context arises more from the temporal interaction between elements than from their connective interface proximity.
A classic example of the thinking that results when we don’t understand this boundary of “context” within neural behavior, is the curious concept which has arisen in neuroscientific research, a conceptualization referred to as “the grandmother cell”: In an (ultimately vain) effort to attach the objectification of sensory experience to smaller and smaller granularities of neural organization, researchers took it to the limit and hypothesized the existence of individual neurons, called “gnostic neurons”, that would individually respond to holistic external objects in the environment, (say, for instance, a cell that would individually signal the recognition of your grandmother).
When neuroscientific researchers promote the conceptual position that individual neurons themselves exchange “information”, we find this intellectual demand results in concepts that cannot possibly model the true resolution of “context” in the neural experience.
This constrained thinking, brought on by a confusion between the concepts of signaling and information, stretches way back to influence the very genesis of our human logic systems, which is reflected in the development of a logic that has been, for centuries, wholly devoid of a singular existential quantifier, that key device that gives the reasoner the ability to logically point to “that thing”, even before “that thing” has been semantically defined. (A deficiency corrected in the Logic of Infinity).
So how does the TSIA engineer develop the needed concepts to sort this all out?
In the introduction to the Organon Sutra, the discussion touched on that Great Fact of Life, that nothing in life comes free. And when it comes to the human mind, and indeed the complexes we desire to see emerge in our TSIA, the assimilation of every unit of knowledge comes at a cost, which in an indirect way, can be said to place a value, or (in the lexicon of basic accounting), a liability on all assimilated knowledge.
This basic economics lesson of Life has been variously termed ‘neural biasing’, or ‘neural entropy’, where the creation of long-term structures in neuron organization have the effect of narrowing the options for, or “biasing”, the creation of future structures.
Neural biasing means that, in the course of adaptation by any organism, each incremental increase in knowledge assimilation into the organism must be paid for by a correspondingly incremental decrease in the freedom with which an organism can deal with the assimilation of new knowledge. In this temporal cycle, we can envision how knowledge becomes structure, and that structure further defines the scaffolding for understanding subsequent knowledge. So, to extend the economics metaphor of neural biasing somewhat, when knowledge becomes structure, it becomes both an asset and a liability. It is an asset in its ability to “format for” future knowledge, and it is a liability in its constraint of future structures. (Geez, is there no end to the circular dualities in natural intelligence?)
Neural biasing creates a static asset to knowledge collection, (found in created neural structures), but that structure also creates a temporal liability to the range of new knowledge obtainable.
(Again, it is because of the temporality in this “knowledge biasing” that we cannot resolve a definition in the temporal aspects of “information” based on neural connectivity alone, even at higher levels of neural organization).
While pursuing this analogy of the valuation that evolution has placed on knowledge assimilation, the dialog introduced a fundamental conceptualization of knowledge itself, but this knowledge wasn’t defined so much as a product, it was conceptualized by the process which resolves that product.
Now, this characterization of knowledge biasing is viewed from the perspective of an organisms’ ongoing adaptation to an environment over its lifetime, but if we can conceptually telescope the temporal perspective of this characterization to just the individual process in a singular event of “knowledge assimilation”, we may get closer to a description of neural behavior, but then our terminology becomes a bit more fuzzy, so it is necessary for the TSIA engineer to become more adept in the “temporal scoping” of her thinking.
We can do this by recognizing an analogy between “knowledge becoming structure” at the macro level, and how it relates to our conceptualization at the ground level where signaling becomes “information”, followed by the temporal process which promotes the transformation of new signaling into richer “information”.
In every sense of their expression, our thoughts would be useless if, after having expressed them, our mind returned to the same state it was in before their expression. Every thought changes our mind into something that it wasn’t before. Because of this, we should not conceive of our thoughts as things, but as processes.
It is this temporal process in adaptation that the TSIA engineer must focus on.
Which is difficult when the TSIA engineer gets stuck when interpreting the various levels to this temporality, as the perspective moves from the ground level of individual neurons to the level of neural assemblies, and then to the macro level of neural behavior, or even to higher levels of global neural organization.
This difficulty most times arises when the TSIA engineer confuses the interconnection of neurons with their temporal behavior, a confusion which is hard to shake until the TSIA engineer shakes the preconceived notion that there is some hierarchical design intent behind the interconnection of a biological neural complex (or a synthetic, massively asynchronous assembly).
Now, certainly Nature does not craft the interconnections between her neural creations just willy-nilly. But to grasp how the interconnections between neurons come to be, the TSIA engineer must envision the temporal behavior of neural organizations not from a top-down perspective, but from the continuous circularity of a massively asynchronous assembly that has no beginning or end.
So let’s try to begin this circular thinking by closing our “top-level” concepts in on those “bottom-level” concepts, to form a continuous circle of ground-level concepts.
Returning to the dialog at the beginning of the Organon Sutra, the discussion went on to say that, in the real world, there is no physical force that correlates Time and Space, it is only the abstract fancy of Man that deems to establish that correspondence, the act of which becomes the fundamental process from which all other intellectual activity follows.
This act was characterized by postulating the scenario that, surely, even the meager intellectual proficiency of Early Man could make the mental leap of connecting the setting of the Sun with the cooling of the evening air, and thus bridging two separate perceptions in time into one singular spatial concept, however primitive that concept might have been.
For sure, this must certainly be the “top-level” conceptualization we envision for intelligent behavior, whether biological or synthetic, because it is the process of this abstract correlation of Time and Space, this fundamental process, that has freed the Homo Sapiens species from the neurological tyranny imposed on the mammalian central nervous system by that liability of the entropic rule of neural biasing, a freedom which has set humans apart in their behavior from all other mammalian species.
This “top-level” concept (of the abstract correlation of Time and Space) folds in on itself into a circularity when the TSIA engineer realizes that it manifests itself at the lowest level of neurological ontogeny. This abstract correlation, this cognitive fusion of Time and Space, must also occur at the very elementary level of individual neurons themselves (or, in the case of our TSIA, at the lowest level of synthetic signaling elements), in an elementary fusion of time and signaling.
Where the idiom of contemporary digital computing devices divide the processes of compute-and-store across separate computing elements, the idiom of synthetic intelligent computing must combine the processes of compute-and-store into the singular, elementary intelligent computing unit, in order to express that temporal fusion of time and signaling throughout the entire circularity of organic and synthetic adaptation.
Temporality must now enter into the “computation” of our intelligent digital machine, instead of being distributed throughout the storage mechanism. So, it should be now apparent that the path to digital intelligence lies in a design paradigm which moves that temporality (implicit in data location) away from data storage, into the very mechanism of digital computation itself.
And as was stated at the beginning of this chapter, we can envision that new paradigm within the Von Neumann digital architecture, (defined as one having a single accumulator per clock cycle), by imagining an implementation of the infinite accumulator, which represents the hardware complement to the Logic of Infinity.
